ответ:
наибольшее и наименьшее значение функции на отрезке надо искать среди ее экстремумов и на границах отрезка.
найдем экстремумы функции y= \frac{3}{2} x^{2/3}- \frac{1}{3}x^3y=
2
3
x
2/3
−
3
1
x
3
y'= \frac{3}{2} *\frac{2}{3} x^{-1/3}- \frac{1}{3}*3x^2=x^{-1/3}- x^2=0y
′
=
2
3
∗
3
2
x
−1/3
−
3
1
∗3x
2
=x
−1/3
−x
2
=0
x^{-1/3}= x^2x
−1/3
=x
2
x=0, x=1
проверяем точки 0, 1 и 8 (границу отрезка)
y(0)=0
y(1)=3/2-1/3=(9-2)/6=7/6=1 1/6
y(8)=y= \frac{3}{2} 8^{2/3}- \frac{1}{3}8^3=\frac{3}{2} *4- \frac{1}{3}*512=6 - 170 \frac{2}{3}= -164 \frac{2}{3}y=
2
3
8
2/3
−
3
1
8
3
=
2
3
∗4−
3
1
∗512=6−170
3
2
=−164
3
2
ответ: y(8)=-164 2/3 -наименьшее значение, а y(1)=1 1/6 -наибольшее значение на отрезке [0; 8]
Сначала сократить как обычную дробь. Тут получиться три пары чисел, которые можно сократить: 1,7 и 5,1; 4,92 и 0,82; 7,2 и 4,8. Сокращать можно, если оба числа возможно поделить на одну и ту же цифру (например 1,7 и 5,1 можно поделить на 1,7, то есть получится 1 и 3 соответственно. Теперь, в дроби, вместо 1,7 будет стоять 1, а вместо 5,1 будет 3)
Сокращаем и получаем:
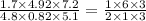
Дальше все числа в числителе и знаменателе перемножаем, чтобы получить только одно число сверху, и только одно снизу:
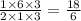
Из получившейся дроби пробуем вынести целое число:
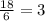
Всё, пример решён, ответ 3
6/4=1.5
Скорость вырастет в 1.5 раза