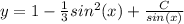
Пошаговое объяснение:
y'tgx + y = cos²x
Решаем методом вариации постоянной (Лагранжа).
Шаг 1. Решение однородного уравнения
y'tgx + y = 0
Делим обе части уравнения на y·tgx
y'/y + ctgx = 0
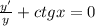
dy/y = -ctg(x)dx
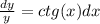
Интегрируем обе части уравнения
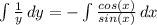
ln|y| = -ln|sin(x)| + ln|C|
ln|y| = ln|C/sin(x)|
y = C/sin(x)
Шаг 2. Заменяем постоянную С на функцию u(x)
y = u(x)/sin(x)
Находим производную
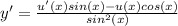
Подставляем в исходное дифференциальное уравнение
y'tgx + y = 0
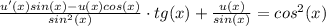
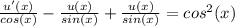
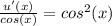
u'(x) = cos³(x)
du = cos³(x)dx
Интегрируем обе части уравнения
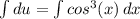
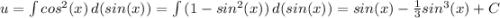
u(x) = sin(x) - sin³(x)/3 + C
Решение уравнения
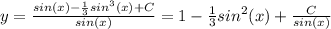
Чётное число - это 2k при любых значениях k. Подставим наше чётное число в выражение вместо n:
(2k)³-2k=8k³-2k - коэффициенты при k - чётные числа, значит и само значение выражения - чётное число.
Нечётное число - это 2k+1 при любых значениях k. Подставим наше число в выражение. Получим:
(2k+1)³-(2k+1)=(2k)³+3*(2k)²*1+3*2k*1²+1³ - 2k-1=8k³+12k²+6k+1-2k-1=
=8k³+12k²+4k - коэффициенты при k - чётные числа, значит и само значение выражения - чётное число.