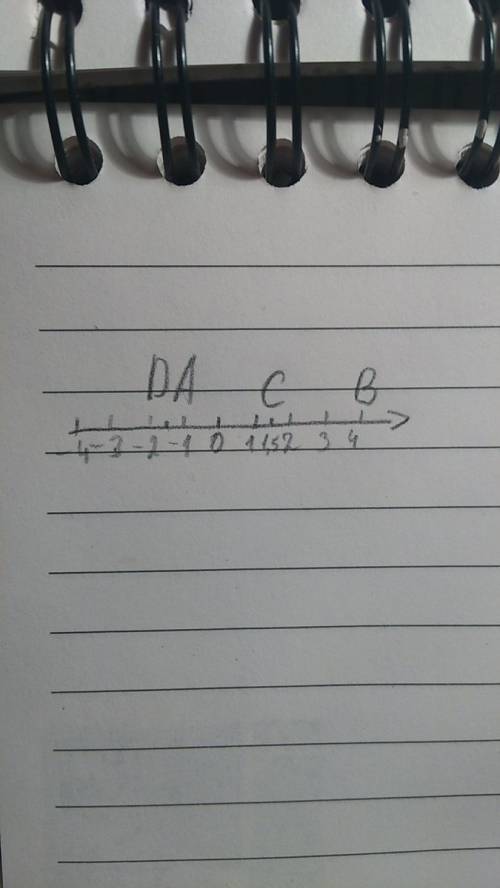
Возраст волшебника 12087 лет.
Пошаговое объяснение:
Требуется найти пятизначное число, в котором все цифры разные, а трехзначное число, стоящее между крайними цифрами, делится на 13.
1) По условию первая цифра в 7 раз меньше последней. ⇒ Первая цифра в числе не может быть больше единицы, иначе последняя цифра будет двузначной (2*7 = 14) и мы выйдем за рамки пятизначных чисел. ⇒ Первая цифра = 1, последняя цифра = 7.
Исходное число имеет вид 1 * * * 7.
2) Между цифрами 1 и 7 стоит трехзначное число, которое делится на 13. Его можно представить как 13n, n ∈ Z (n - целое число).
По условию в исходном числе все цифры разные, поэтому это трехзначное число не может принадлежать первой сотне трехзначных чисел, так как цифра 1 у нас уже есть. ⇒
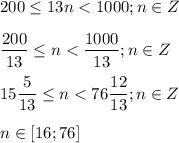
⇒ при n = 16 число 13n = 13*16 = 208. Число 208 наименьшее допустимое трехзначное число, удовлетворяющее условию задачи.
Тогда исходное число 12087.
В тетради записаны 5 подряд идущих целых чисел
x, x+1, x+2, x+3, x+4
Пусть вычеркнули число x+n , где n может быть 0;1;2;3 или 4.
Тогда сумму всех пяти чисел можно записать уравнением
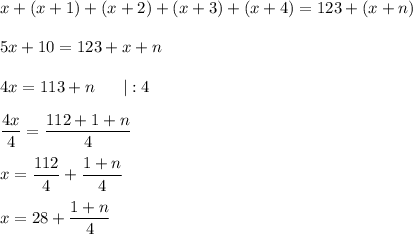
Число х по условию целое, тогда дробь 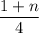 тоже должна стать целым числом, то есть сумма
тоже должна стать целым числом, то есть сумма 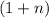 будет кратна числу 4.
будет кратна числу 4.
Из возможных значений числа n (0; 1; 2; 3; 4) подходит только 3.
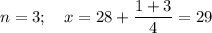
В тетради были записаны числа 29, 30, 31, 32, 33
Вычеркнуто число 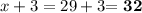
-----------------------------------------
Проверка :
29 + 30 + 31 + 33 = 123
ответ : 32