Найдем вероятность того, что при восьми бросках ни разу не выпадет простое число очков.
При единичном броске эта вероятность равна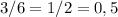 
(так как всего результатом могут стать шесть цифр: 1, 2, 3, 4, 5, 6; а простых из них всего лишь три: 2, 3, 5).
А так как бросков было совершено восемь, то:
P (ни разу не выпадет простое число очков) =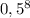 
.
Заметим, что мы искали вероятность события, противоположного искомому. Поэтому вероятность искомого события равна:
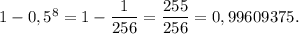
Найдем вероятность того, что ни разу не выпадет ни 1 очко, ни 6 очков.
При единичном броске мы имеем четыре благоприятствующих исхода (2, 3, 4, 5) из шести возможных (1, 2, 3, 4, 5, 6). Вероятность равна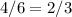 
.
При восьми бросках, естественно, получается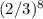 
.
И вероятность искомого события (противоположного рассматриваемому) равна:
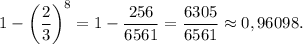
2, 1200/120=10 дм/с скорость мальчика при спуске
примечание: таких высоких деревьев не бывает.