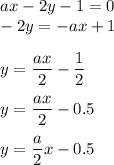
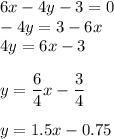
а) Если даны две функции, у которых коэффициент k (стоящий перед x) равен, то графики этих функций будут параллельны.
У первой функции k = a/2, у второй - 1,5. Для того, чтобы коэффициенты были равны, нужно подставить такое значение a, чтобы при делении на 2 оно давало 1,5.
В таком случае, a = 3.
б) Если даны две функции, не имеющих равных коэффициентов k и m (то есть она не будут параллельны или одна функция не равна другой), то у графиков этих функций будет одна общая точка. В таком случае, a может принять любое значение, кроме 3 (иначе графики будут параллельны).
То есть, 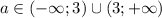
10.
(4•√3)^2 / 2√3 =
= (4√3 • 4√3) / 2√3 =
= (4√3) • 2 = 8√3
ответ: А) 8√3
11.
1) -1,3х^2 + 4,2х = 0
-0,1х(13х - 42) = 0
Либо -0,1х = 0
х = 0/(-0,1)
х = 0
Либо
13х - 42 = 0
13х = 42
х = 42/(13)
х = 3 3/13
2) 1,3х^2 - 4,2х = 0
0,1х(13х - 42) = 0
Либо 0,1х = 0
х = 0/0,1
х = 0
Либо
13х - 42 = 0
13х = 42
х = 42/(13)
х= 3 3/13
3) -1,8х^2 - 4,2 = 0
-0,6(3х^2 + 7) = 0
3х^2 + 7 = 0/(-0,6)
3х^2 + 7 = 0
3х^2 = -7
х^2 = - 7/3 - корней нет - квадрат числа не может быть отрицательным.
4) 1,8х^2 - 4,2 = 0
0,6(3х^2 - 7) = 0
3х^2 - 7 = 0/(0,6)
3х^2 - 7 = 0
3х^2 = 7
х^2 = 7/3
х^2 = 2 1/3
х = √(2 1/3)