ассмотрим такой пример. Нужно последовательно посчитать: .
Можно переставить вперед числа, которые необходимо складывать, а затем выполнить вычитание оставшихся: .
Но это не всегда удобно. Например, мы можем вычислять остаток вещей на каком-нибудь складе и нам необходимо знать промежуточный результат.
Можно выполнять действия и подряд: .
Мы знаем, что , значит, результатом будет вычитание из числа . Это значит, что надо вычесть , но пока не из чего. Когда будет из чего вычесть, вычтем:
.
Но мы можем «схитрить» и обозначить . Таким образом, мы введем новый объект – отрицательные числа.
Такую операцию мы уже проделывали – в природе, например, числа «» тоже не существовало, но мы ввели такой объект, чтобы облегчить запись действий.
Пошаговое объяснение:
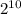рассадки членов жюри.
