На уроке было дано сделать и раскрасить чертеж, на котором изображены три фигуры: круг, квадрат и треугольник.у каждого из 20 учеников класса есть по четыре цветных карандаша: красный , синий, зеленый и желтый.каждую фигуру на четреже можно раскрашивать любым цветом, но цвет фигур не должен повторяться. могут ли ученики этого класса выполнить раскраску так, что бы все их чертежи отличались друг от друга.?

👇

Увидеть ответ

Ответ:

on82

08.11.2022

Неможуть тому що 5 учнів розфарбує однаково
P.s я невпевнена

4,8(11 оценок)

Ответ:

Яяяячччч

08.11.2022

Мне кажется не смогут

4,6(15 оценок)

Открыть все ответы

Ответ:

dimadementev2

08.11.2022

А 360 км В

> 28 км/ч t = 6 ч ? км/ч <

по действиям).

1) 28 · 6 = 168 (км) - проедет один фельдшер за 6 ч;

2) 360 - 168 = 192 (км) - проедет другой фельдшер за 6 ч;

3) 192 : 6 = 32 (км/ч) - скорость другого фельдшера.

Выражение: (360 - 28 · 6) : 6 = 32.

Или так:

1) 360 : 6 = 60 (км/ч) - скорость сближения;

2) 60 - 28 = 32 (км/ч) - скорость другого фельдшера.

Выражение: 360 : 6 - 28 = 32.

уравнение).

Пусть х км/ч - скорость другого фельдшера, тогда (х + 28) км/ч - скорость сближения. Уравнение:

(х + 28) · 6 = 360

х + 28 = 360 : 6

х + 28 = 60

х = 60 - 28

х = 32

ответ: 32 км/ч.

4,4(89 оценок)

Ответ:

1Юліана1

08.11.2022

(a + 1)(b + 1)(a + b) = 2020 ⇔ (b + 1)(a + 1)(b + a) = 2020

В уравнении не важно a≥b или b≥a.

Так как решить нужно в целых числах, то без разложения на множители не обойтись.

2020 = 1 · 2 · 2 · 5 · 101

Легко проверить, что a и b не могут принимать значения 0 и ±1. Значит, |a|>1 , |b|>1 и наибольшим множителем будет

| a+b | = 101

Возможные варианты модулей множителей (без учёта знаков) :

2020 = 1 · 20 · 101 = 2 · 10 · 101 = 4 · 5 · 101

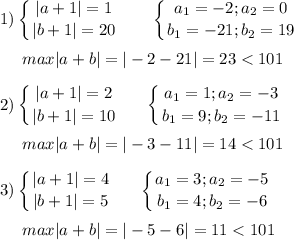
$\displaystyle 1) \left \{ {{ |a+1|=1} \atop {|b+1|=20}} \right.~~~~~\left \{ {{ a_1=-2;a_2=0} \atop {b_1=-21;b_2=19}} \right.\\\\~~~~~max |a+b|=|-2-21|=23$

Вывод : уравнение (a + 1)(b + 1)(a + b) = 2020 не имеет решений в целых числах.

===========================================

Возможно, в условии опечатка

(a + 1)(b + 1)(a + b) = 20 ⇔ (b + 1)(a + 1)(b + a) = 20

В уравнении не важно a≥b или b≥a.

20 = 1 · 2 · 2 · 5

Возможный порядок модулей множителей (без учёта знаков) :

20 = 1·2·10 = 1·4·5 = 2·2·5 = 1·5·4 = 1·10·2 = 4·5·1 = 2·10·1

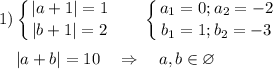
$\displaystyle 1) \left \{ {{ |a+1|=1} \atop {|b+1|=2}} \right.~~~~~\left \{ {{ a_1=0;a_2=-2} \atop {b_1=1;b_2=-3}} \right.\\\\~~~~|a+b|=10~~~\Rightarrow~~~a,b\in\varnothing$

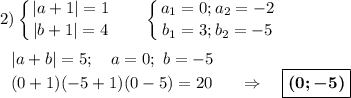
$\displaystyle 2) \left \{ {{ |a+1|=1} \atop {|b+1|=4}} \right.~~~~~\left \{ {{ a_1=0;a_2=-2} \atop {b_1=3;b_2=-5}} \right.\\\\~~~|a+b|=5;~~~a=0;~b=-5\\~~~(0+1)(-5+1)(0-5)=20~~~~~\Rightarrow~~~\boxed{\boldsymbol{(0;-5)}}$

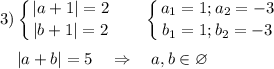
$\displaystyle3) \left \{ {{ |a+1|=2} \atop {|b+1|=2}} \right.~~~~~\left \{ {{ a_1=1;a_2=-3} \atop {b_1=1;b_2=-3}} \right.\\\\~~~~|a+b|=5~~~\Rightarrow~~~a,b\in\varnothing$

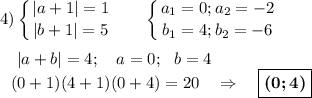
$\displaystyle 4) \left \{ {{ |a+1|=1} \atop {|b+1|=5}} \right.~~~~~\left \{ {{ a_1=0;a_2=-2} \atop {b_1=4;b_2=-6}} \right.\\\\~~~~|a+b|=4;~~~a=0;~~b=4\\~~~(0+1)(4+1)(0+4)=20~~~\Rightarrow~~~\boxed{\boldsymbol{(0;4)}}$

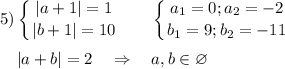
$\displaystyle 5) \left \{ {{ |a+1|=1} \atop {|b+1|=10}} \right.~~~~~\left \{ {{ a_1=0;a_2=-2} \atop {b_1=9;b_2=-11}} \right.\\\\~~~~|a+b|=2~~~\Rightarrow~~~a,b\in\varnothing$

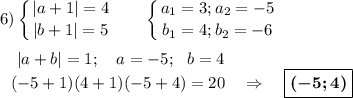
$\displaystyle 6) \left \{ {{ |a+1|=4} \atop {|b+1|=5}} \right.~~~~~\left \{ {{ a_1=3;a_2=-5} \atop {b_1=4;b_2=-6}} \right.\\\\~~~~|a+b|=1;~~~a=-5;~~b=4\\~~~(-5+1)(4+1)(-5+4)=20~~~\Rightarrow~~~\boxed{\boldsymbol{(-5;4)}}$

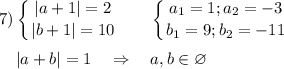
$\displaystyle7) \left \{ {{ |a+1|=2} \atop {|b+1|=10}} \right.~~~~~\left \{ {{ a_1=1;a_2=-3} \atop {b_1=9;b_2=-11}} \right.\\\\~~~~|a+b|=1~~~\Rightarrow~~~a,b\in\varnothing$