7
Пошаговое объяснение:
Вспомним признак делимости на 9: число делится на 9 тогда и только тогда, когда его сумма цифр делится на 9.
Этот признак работает и для равноостаточности при делении на 9. То есть, число и его сумма цифр имеют одинаковый остаток при делении на 9.
Пусть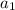 
- изначальное число и 
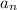- сумма цифр числа 
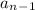. Пусть остаток при делении на 9 у числа 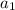- r, тогда и у числа 
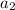остаток при делении на 9 тоже r. Но тогда и у чисел 
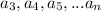остаток при делении на 9 равен r. Но так как r - чисто от 0 до 9, то это и есть наша оставшаяся в конце цифра.
Тогда нам нужно всего лишь найти остаток при делении на 9 у числа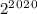 
. А он такой же, как у числа 
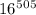, и такой же, как у числа 
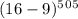, и такой же, как у числа 
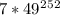, а он такой же, как у числа 
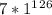, а это равно 7.
ответ:на 5 минут Настя выполнила это задание раньше чем Даша.