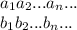
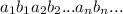
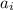равен 2i-1
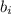равен 2i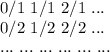
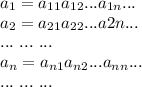
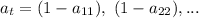
а) на доске выписаны числа 1, 2, 4, 8, 16, 32, 64, 128. разрешается стереть любые два числа и вместо них выписать их разность – неотрицательное число. после семи таких операций на доске будет только одно число. может ли оно равняться 97?
б) на доске выписаны числа 1, 21, 2², 2³, 210. разрешается стереть любые два числа и вместо них выписать их разность – неотрицательное число. после нескольких таких операций на доске будет только одно число. чему оно может быть равно?
решение
a) получить 97 можно, например, так. последовательно вычитая из 16 числа 8, 4, 2, 1, получим 1. на доске остались числа 1, 32, 64, 128. далее: бикю 64 – 32 = 32, 32 – 1 = 31, 128 – 31 = 97.
б) докажем, что если на доске выписаны числа 1, 2, 2n, то после n операций, описанных в условии, может получиться любое нечётное число от 1 до 2n – 1. очевидно, числа, большие 2n, на доске не появляются. легко видеть также, что на доске всегда присутствует ровно одно нечётное число. значит, и последнее оставшееся на доске число нечётно. утверждение о том, что все указанные числа построить можно, докажем индукцией по n.
база. имея числа 1 и 2, можно получить только число 1.
шаг индукции. пусть на доске выписаны числа 1, 2, 2n+1. любое нечётное число, меньшее 2n, можно получить за n + 1 операцию (на первом шаге сотрём 2n+1 и 2n и напишем 2n, далее по предположению индукции). нечётные числа от 2n + 1 до 2n+ 1 – 1 можно записать в виде 2n+1 – a, где число a можно получить из набора 1, 2, 2n. на последнем шаге из 2n+1 вычитаем a.
ответ
а) может; б) любому нечётному числу от 1 до 210 – 1.
замечания
: 2 + 3
А•73=35697
А=35697:73
А=489
ответ:489