Эта задача на доказательство решается применением "принципа Дирихле". В самом простом варианте этот принцип звучит так: если 11 кроликов рассадить в 10 клеток, то по крайней мере в одной клетке окажутся 2 кролика.
В нашей задаче, дни недели - это "клетки", их 7 (с понедельника по воскресенье), а 22 ученика - это "зайцы".
Доказательство: Очевидно, что 22:7=3 (ост.1). Это означает, что если бы в каждый день недели рождалось по 3 человека, то остался еще 1 остался бы "без дня пождения". Значит т.к. у нас 22 ученика имеют день рождения, то по крайней мере 4 из них - рождены в один день недели, что и требовалось доказать.
Зная длины сторон треугольника можно вычислить его плошадь по формуле Герона:
S = √ (p×(p-a)×(p-b)×(p-c)), где
p - полупериметр
a, b, c - длины треугольника
1) р =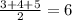 см
см
2) S = √ (6×(6-3)×(6-4)×(6-5))= √ (6×3×2×1) = √36 = 6(см²)
ответ: 6(см²)