Question

1)во время весеннего паводка изменение объема поступающей в озеро воды в течение суток можно описать уравнением s(t)=10+4t гдеs(t) – объем поступившей в озеро воды (в м3) за время t (в часах), 0

Answer 1

S(t) это объем поступившей воды. Известно из условия

Пусть x(t) это будет скорость стока воды

x(t)=58

Чтобы найти объем в любой момент времени нужно из объема поступающей воды (у нас он равен S(t) вычесть объем вытекающей воды, его надо найти)

Обозначит объем вытекающей воды y(t), тогда справедливо следующее уравнение:

$x(t)=\frac{dy(t)}{dt}$

 Теперь отсюда найдем y(t):

$x(t)=\frac{dy(t)}{dt} \\ x(t)dt=dy(t) \\ \int{x(t)}\, dt=\int{dy(t)}\, dt \\ \int{x(t)}\, dt=y(t) \\y(t)=\int{x(t)}\, dt$

 Теперь собственно найдем интеграл:

$x(t)=58 \\ \\ y(t)=\int{58}\, dt=58t+C$, где C=const

Теперь запишем общий вид уравнения для нахождения V(t)

V(t)=S(t)-y(t)

$V(t)=10+4t-58t-C=10-54t-C$

Теперь надо найти чему равна С. Нам известно что V(0)=30 000, воспользуемся этим фактом:

$V(0)=10-54\cdot 0-C=30 000 \\ 10-C=30 000 \\ C=-29 990$

Подставим в наше уравнение:

$V(t)=10-54t+29990=30000-54t$

 Таким образом получаем, что математическая модель для нахождения V(t) имеет вид:

  $V(t)=30000-54t$ 

 2) Найдем объем воды при t=6

 $V(6)=30000-54\cdot 6=29676$ м3

 3) Объем воды при t=16

$V(16)=30000-54\cdot 16=29136$ м3

4)  )Если в момент времени t=18 сток воды из озера был перекрыт и до конца суток воды из озера не вытекала. Найдем объем воды на конец дня.

Сначала найдем объем воды на момент  t=18

$V(18)=30000-54\cdot 18=29028$ м3

 Поскольку вода не вытекает, то объем воды в озере будет только прибывать. Значит математическая модель будет иметь вид:

V(t)=S(t)=10+4t

 Вода прибывала 24-18=6 часов, значит надо вычислить какой объем воды втек за 6 часов

V(6)=10+4*6=34 м3

Значит на конец дня объем воды будет  29028+34=29 063 м3

 1)   $V(t)=30000-54t$ 

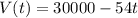
 2)

 а)  29 676 м3

 б)  29 136 м3 

 3)  29 063 м3