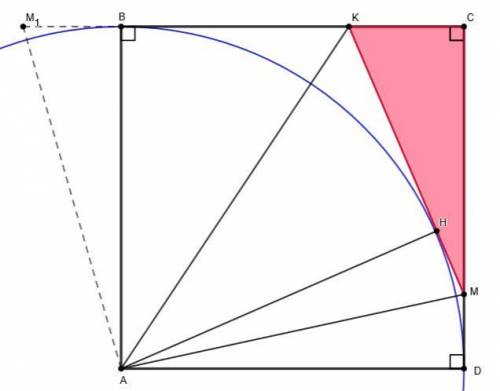
Условие: На сторонах ВС и CD квадрата ABCD взяли точки K и M так, что ∠MAK = 45°. Известно, что KM = 13 ,KC = 5 ,CM = 12. Найдите сторону квадрата ABCD.
Дано: K ∈ BC, M ∈ CD, ∠MAK = 45°, KM = 13 ,KC = 5 ,CM = 12.
Найти: BC.
Осуществим поворот ΔAMD на 90° против часовой стрелки ⇒ ΔAMD переходит в ΔAM₁B, ΔAMD = ΔAM₁B.
∠BAD = ∠BAK + ∠MAK + ∠MAD = 90° ⇒ ∠BAK + ∠MAD = 90° - ∠MAK = 90° - 45° = 45°
Из равенства ΔAMD = ΔAM₁B следует, что ∠MAD = ∠BAM₁, значит, ∠BAK + ∠BAM₁ = 45°.
ΔMAK = ΔM₁AK по двум сторонам и углу между ними:
AM = AM₁ - так как ΔAMD = ΔAM₁BАК - общая сторона∠MAK = ∠M₁AK = 45°Отсюда следует, что ∠АКМ = АКМ₁.
Аналогичным образом, осуществив поворот ΔAВК на 90° по часовой стрелке, можно утверждать, что ∠AMK = ∠AMD.
Заметим, что биссектрисы АК и АМ внешних углов при вершинах К и М ΔКСМ пересекаются в точке А, то есть точка А является центром вневписанной окружности ΔКСМ ⇒ AB = AD = AH - радиусы вневписанной окружности.
КВ = КН, MD = MH - как отрезки касательныхBC + СD = (BK + CK) + (CM + MD) = (KH + CK) + (CM + MH) = CK + CM + (KH + MH) = CK + CM + MK = 5 + 12 + 13 = 30
BC + СD = 30 ⇒ BC + BC = 30 ⇒ BC = 15
ответ: 15.
94×3=282 км за 3 часа
846-282=564 км