Обозначим четыре части: a; b; c; d.
По условию:
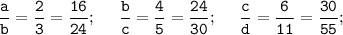
Очевидно, что а = 16; b = 24; c = 30; d = 55
a + b + c + d = 16 + 24 + 30 + 55 = 125
Первая дробь: числитель и знаменатель умножаем на 8, вторая - на 6, третья - на 5. Такой выбор множителей нужен для того, чтобы уравнять значение b, в первом и втором соотношении, и значение с - во втором и третьем соотношении.
Сумма частей, полученная при этом, не обязательно будет равняться исходному числу, но, в любом случае, она будет ему кратной.
Например, исходное число при тех же соотношениях между частями, равно 375. Так как мы в сумме получили 125 "микрочастей", то каждая такая часть, в этом случае, равняется 3, и число 375 разбивается на:
16*3 + 24*3 + 30*3 + 55*3 = 48 + 72 + 90 + 165 = 375.
=========================
Для тех, кто, все-таки, решает эту задачу уравнением..))
Воспользуемся основным свойством пропорции:
3a = 2b; 5b = 4c; 11c = 6d
Сложим левые и правые части:
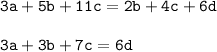
Постараемся в левой части оставить выражение, кратное a+b+c+d, которое, по условию, равно 125:

ответ: 16; 24: 30; 55.
х тг - получит каждый человек за 1 рабочий день
х·8·4 = 32х тг - получит первая бригада за 4 рабочих дня
х·11·5 = 55х тг - получит вторая бригада за 5 рабочих дней
По условию две бригады всего получили 261 000 тг, получаем уравнение:
32х + 55х = 261000
87х = 261000
х = 261000 : 87
х = 3000 тг - получит каждый человек за 1 рабочий день
3000 · 32 = 96 000 тг - получит первая бригада за 4 рабочих дня
3000 · 55 = 165 000 тг - получит вторая бригада за 5 рабочих дней
ответ: 96 000 тг; 165 000 тг -
7/16-5/24=21-10/48=11/48
2/11-1/12=24-11/132= 13/132
12/13-15/26= 24-15/26=9/26
9/28-11/35=315-308/980=7/980=1/140
39/40-19/28=1092-760/1120= 332/1120=83/280
25/28-18/35= 875-504/980= 371/980=53/140
40/63-35/72= 320-245/504=75/504=25/168
22/21-21/22=484-441/462= 43/462