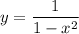
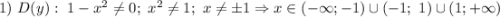
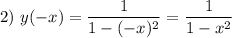 — функция является четной и непериодической.
— функция является четной и непериодической.
 Если
Если 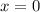 , то
, то 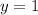 , значит
, значит 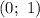 — точка пересечения с осью ординат. Если
— точка пересечения с осью ординат. Если 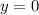 , то есть
, то есть 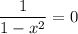 , то
, то  , значит нет точек пересечения с осью абсцисс.
, значит нет точек пересечения с осью абсцисс.
 Поскольку
Поскольку 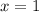 и
и 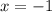 — точки разрыва функции и
— точки разрыва функции и 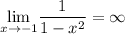 и
и 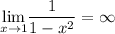 , то
, то
Если 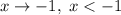 , то
, то 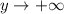 ; если
; если 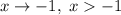 , то
, то 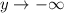
Если 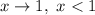 , то
, то 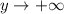 ; если
; если 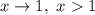 , то
, то 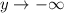
Найдем наклонные асимптоты 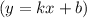 :
:
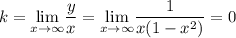
Если 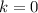 , то имеем горизонтальную асимптоту. Найдем
, то имеем горизонтальную асимптоту. Найдем 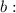
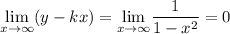
Следовательно, 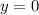 — горизонтальная асимптота.
— горизонтальная асимптота.
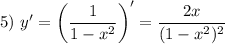
Из уравнения 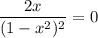 имеем критическую точку функции:
имеем критическую точку функции: 
Заполним таблицу №1 (см. вложение).
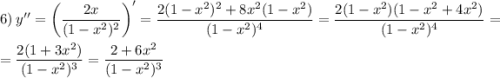
Если 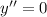 , то
, то 
Систематизируем данные, полученные по второй производной, в таблице №2 (см. вложение).
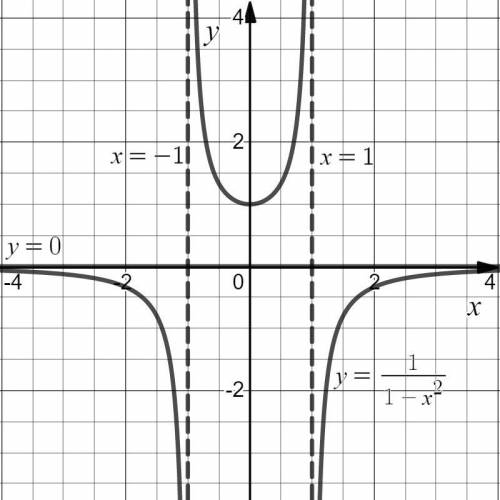
Для достоверности изобразим полученный график (см. вложение).
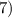 Из рисунка видим, что
Из рисунка видим, что 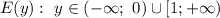

1. Багато горя зазнала Малуша, а передумала стільки, що коли б тими думками землю засіяти, то вже все поле і шляхи від Росі до Києва проросли б шипшиною і тернями [складнопідченене речення, однорідні присудки] (с. Скляренко).
2. Мені мабуть не докучити нагадувати, що хто не знає свого минулого, той не гідний свого майбутнього [складнопідрядне речення] (Н. Рильський).
3. Як радісно мені, що знову сніг розтане і зелене вбрання одягнуть дерева [сложноподчененное пропозицію] (в.Сосюра). 4. Сергія не влаштовує, як футболісти ходять самовпевнено і свистять в коридорах, і важаться після кожного тренування, і під час дощу, зібравшись у вестибюлі, крейдою на чорній дошці забивають уявні голи у ворота суперника [складнопідченене речення, дієприслівниковий оборот, однорідні присудки] (а.Гончар).
5. Соломія міркувала, що коли брати зліва Плавні повинні швидко скінчитися [складнопідченене речення] (м.Коцюбинський).
Четвертое79*68+435268=440640
Шестое 440640-558=440082