1. |−27| = 27 (модуль - всегда только положительное число)
2. а) -a = 7,3
б) -a = -85
3. правило: минус на минус дает плюс; минус на плюс дает минус.
а) -18
б) +34
4. |-10,5| = 10,5 (правило выше)
|143| = 143
5. а) 316 > -316
б) -5,32 > - 5,2 (смотрим по первой цифре после запятой)
6. а) 5,7 + ( - 6) = 5,7 - 6 = -0,3
б) – 10 – 6 ∙ (-1,5) = -10 + 9 = -1
7. а) - 3,2 : 0,8 = -4
б) - 45 ∙ ( - 516 ) = 23220
в) (- 9) : ( - 13 ) = 9/13 (типа это дробь)
г) (-1) ∙ (-0,01) = 0,01
8. а) (−13)2 = -26
б) – 10 – 6 ∙ (-1,5) = -10 + 9 = -1
в) −4,5−7−3 = -4,5-10 = -14,5
9. −0,8+2,26−8,1 = 1,46-8,1 = -6.64
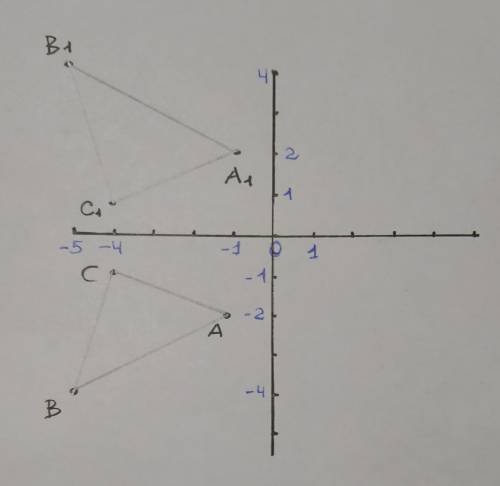
10. Координаты: A₁(-1;2), B₁(-5;4), C₁(-4;1)
(см. файл.)
Пошаговое объяснение:а) Прямые АВ и А₁С₁ - скрещивающиеся, а расстоянием между скрещивающимися прямыми называют расстояние от некоторой точки скрещивающихся прямых (например точки А) к плоскости, проходящей через другую прямую плоскость треугольника АВС), параллельную первой прямой (АС), т.е это есть расстояние между АС и А₁₁С₁.. Оно равно боковому ребру АА₁, ч.т.д. б) 1) Обозначим угол между плоскостями АВС и АКС буквой α =45°. Построим угол α: проведём ВЕ⊥АС и КЕ⊥АС, тогда α= 45°. 2) Так как ВК : В₁К=2 : 3, то ВК=2х, В₁К=3х. 3) Рассмотрим ΔВЕК прямоугольный, т.к. =45°, то он равнобедренный,⇒ВК= ВЕ= 2х , ⇒ЕК²= (2х)²+(2х)²= 8х². 4) ΔАВС по условию равнобедренный, ⇒ АЕ=ЕС= АС/2 = 4√2 : 2= 2√2.Из ΔСЕК -прямоугольного ЕК²= КС² -ЕС² = 8² - (2√2)²= 64 - 8 = 56. 5) Но ЕК²= 8х², ⇒8х² =56, ⇒ х² = 56 :8 = 7, х=√7 6)Тогда искомое расстояние между прямыми АВ и А₁С₁: ВВ₁ =2х+3х=5х= 5·√7 Отв: ВВ₁ =5√7