По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
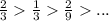
По второму признаку Лейбница предел ряда должен стремится к 0.
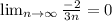
Второе условие Лейбница выполняется. Таким образом, ряд сходится. Исследуем теперь ряд на абсолютной и условной сходимости. Для этого рассмотрим данный ряд по модулю
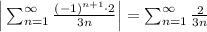
Этот ряд расходится, так как это гармонический ряд и он является расходящимся.
Таким образом, данный исследуемый ряд сходится условно.
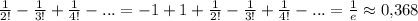
Баланс на 27.07.2012 равен 90
Пошаговое объяснение:
Дата. Расход. Приход. Баланс
01.02.2012. нет 320 =320
05.02.2012 - 185 - =320-185=135
11.02.2012. нет 65 =135+65=200
18.02.2012. -240 - =200-240=-40 ( перерасход)
23.02.2012. нет 270 =-40+270=230
27.07.2012 -140 - =230-140=90
Баланс на 27.07.2012 равен 90 ( ура он положительный, и может на него начисляются проценты)
ответ: 17; 71; 107; 170; 701; 710 вроде все нормально удовлетворяющие условию, так как получить 8 из 7 можно только прибавив единицу