2 задание.
1)натуральные:
9, 24
2)целые:
9,-16,0,24,-50
3)положительные:
9; 1/19 ; 7,2; 4 3/16 ; 24
4)целые отрицательные:
-16, -50
5)дробные отрицательные:
-3,8; -2 6/17
Задание 3.
1)3,1> -6,7
2)-4,2> -4,6
Задание 4.
1)7,3+1,8-3,45 = 5,65 ( модуль раскрывается со знаком + )
2)17/90 : 1 8/9 = 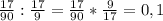
Задание 5.
1)если -х = 25,то х = -25
2)если -(-х)= - 4,9 , то х = -4,9
Задание 6.
1)модуль х = 4,5
х = ±4,5
2)модуль х = -1,8
Такого быть не может,т.к. любое число в модуле положительное,либо равно 0.
Задание 7.
х > -14
Наименьшее целое значение равно
x= -13
Задание 8.
-5,35* < -5,356
Вместо звездочки можно поставить цифры 5,4,3,2,1,0
Задание 9.
Нужно найти такие числа х,которые
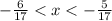
- 0,35294117647 < x < - 0,29411764705
Тогда х = - 0,34 и х = -0,33
Пошаговое объяснение:
Эта задачка не на комбинаторику и теорию вероятности, а на метод от противного. Предположим что у нас на доске менее 3 шашек одного цвета, но тогда шашек другого цвета не менее чем 5-2=3,таким образом мы приходим к противоречию. Значит на доске осталось не менее трех шашек одного цвета. Или так:если положить,что на доске осталось не более двух шашек каждого цвета, то их сумма не больше чем 2+2=4<5,то есть мы приходим к противоречию.Этот будет работать и для большего числа шашек. Для 9 шашек, на доске останется не менее 5 шашек. Для 99 шашек не менее 50. То есть на доске не менее чем (n+1)/2 шашек для нечетного n, и n/2 для четного n одного цвета. n-число шашек,что осталось на доске.