Пусть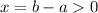 
. Тогда: 
, 
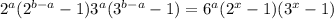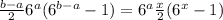, возвращаясь к неравенству и сокращая на 
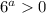, получаем: 
.
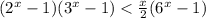Рассмотрим две непрерывные одинаково выпуклые функции. Они могут пересекаться не более чем в одной точке. Действительно, пусть таких точек хотя бы две. Соединим соседние, тогда эта хорда для одной функции располагается над графиком, а для другой — под графиком. Значит, функции разной выпуклости. Следовательно, точек пересечения не более одной.
Легко проверить, что функции, стоящие в обеих частях являются выпуклыми вниз (достаточно дважды продифференцировать или просто раскрыть скобки, разбив функцию на элементарные составляющие).
Графики функции пересекаются в точке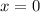 
, значит, для 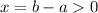они больше нигде не пересекаются. Например, при 
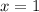неравенство выполнено, стало быть, оно будет выполнено и для остальных положительных 
.
Записать несколько членов последовательности , которая задана ФОРМУЛОЙ ЕЁ n го члена : x=n(n-1)
Тогда 1) х= 1(1-1)=0 2) х=2(2-1) = 2 3) х=3(3-1) = 6 4) х=4(4-1) = 12
и Т.Д.