Пошаговое объяснение:
1 Частные производные для F(x,y,z)=1
dFx=2x, dFy=-2y, dFz=-2z
Значения частных производных в заданной точке - это координаты вектора нормали для касательной плоскости N=(2,4,-4)
Уравнение плоскости A*x+B*y+C*z+D=0
A=Nx=2 B=Ny=4 C=Nz=-4
D=-(Nx*Mx+Ny*My+Mz*Mz)=-(2*1+4*(-2)+(-4)*2)=14
Плоскость 2x+4y-4z+14=0
Нормаль (x-1)/2=(y+2)/4=(2-z)/4
2 Частные производные для F(x,y,z)=2
dFx=2xz-2y^3, dFy=-6xy^2, dFz=12z^3+x^2
Значения частных производных в заданной точке - это координаты вектора нормали для касательной плоскости N=(0,-6,13)
Уравнение плоскости A*x+B*y+C*z+D=0
A=Nx=0 B=Ny=-6 C=Nz=13
D=-(Nx*Mx+Ny*My+Mz*Mz)=-(0*1+(-6)*1+13*1)=-7
Плоскость -6y+13z-7=0
Нормаль (1-y)/6=(z-1)/13
3. Производные на вложенном изображении.
Чтобы перейти к целым числам значения производных в т (1,1,1) домножены на 6.
Вектор нормали тогда N=(3,5,38)
Уравнение плоскости 3x+5y+38z-46=0
Нормаль (x-1)/3=(y-1)/5=(z-1)/38

Пусть на острове x участков 10×40 метров и 16-x участков 20×20 метров.
Периметр каждого участка 10×40 метров равен (10+40)·2 = 100 метров, периметр каждого участка 20×20 метров - 20·4 = 80 метров.
Тогда периметр всех участков 100x+80·(16-x) = 100x+1280-80x = 20x+1280 метров.
На берегах острова заборов нет, значит длина всех заборов на 80·4 = 320 метров меньше периметра всех участков.
20x+1280-320 = 20x+960 м - длина всех заборов.
Но так как между двумя соседними участками забор один, выходит, что мы дважды почитали длины всех заборов. Значит суммарная длина всех заборов равна (20x+960):2 или 540 метров
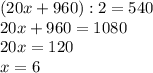
ответ: на острове 6 участков размером 10×40 метров.