№1 1) Можно представить в виде 34-5 и 14-12 Т.к. уменьшаемое 34 больше 14, а вычитаемое 5 меньше 12, то (34-5) больше (14-12) 2) Т.к. в случае -176 и -35 даны отрицательные числа, то их сумма будет отрицательной. В случае же -19 и 21. 21 по значению больше, чем 19, значит сумма будет положительной. Отсюда (-176)+(-35) меньше, чем (-19)+21. №2 На числовой прямой находятся цифры -26,-25,-24...0,1,2,324 Следовательно 26 отрицательных чисел, 0 и 24 положительных числа, итого 51 число. Сумма чисел, имеющих одинаковые значения, но разные знаки равна 0, например (-25) и +25 и т.д. Таким образом сумма целых чисел от -24 до 24 равна 0, остаётся найти сумму чисел (-26) и (-25). Она равна (-51)
1) Точка А =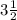
, а точка В = 
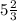⇒ расстояние между ними равно В - А
2) Натуральными числами называют целые числа, использующиеся при счёте
Нужно чтобы числа соответствовали неравенству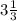
< x < 7
Т.к. 3<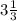
⇒ нам нужна сумма чисел от 4 до 7, то есть 4 ≤ x < 7
4+5+6 = 15
3) Среднее арифметическое находится сложением данных чисел и делением их на их количество
а)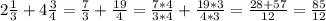
б)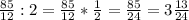
4) Действуем аналогично как в 3 задании
а)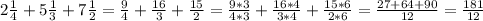
б)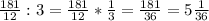
5) Действуем аналогично как в 2 задании
Нужно чтобы числа соответствовали неравенству 1 < x < 47,5
Т.к. 47,5 < 48 ⇒ нам нужно посчитать количество целых чисел от 1 до 47, то есть 1 < x ≤ 47
Их 46