ответ: min y = -3, max y = -1.
Пошаговое объяснение:
Находим производную.
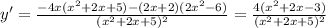
Приравниваем нулю множитель числителя с переменной.
Решаем уравнение x^2+2*x-3=0.
Ищем дискриминант:
D=2^2-4*1*(-3)=4-4*(-3)=4-(-4*3)=4-(-12)=4+12=16;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√16-2)/(2*1)=(4-2)/2=2/2=1;
x_2=(-√16-2)/(2*1)=(-4-2)/2=-6/2=-3.
Находим знаки производной в промежутках между критическими точками.
x = -4 -3 0 1 2
y' = -0,118343 0 0,48 0 -0,118343 .
Как видим, в точке х = -3 минимум функции, а в точке х = 1 - максимум.
Находим значения функции в этих точках.
у(-3) = (-2(9+3))/(9-6+5) = -24/8 = -3.
у(1) = (-2(1+3))/(1+2+5) = -8/8 = -1.
На заданном промежутке [-5; 1] значение функции у(1) = -1 является максимальным, а у(-3) =-3 минимальным.
Всего 27 рыб
щук ? рыб, но на 2 > кар.↓
карасей --- ? рыб, но на 4 < ок.↓
окуней ---? рыб.
Решение.
И щуки, и окуни сравниваются с карасями, щук на 2 рыбины больше, чак карасей, а окуней на 4 больше(т.к. по условию карасей на 4 меньше, чем окуней)
2 + 4 = 6 (рыб.) суммарная разница (настолько других рыб вместе больше, чем карасей)
27 - 6 = 21 (рыб.) --- без разницы (было бы всего рыб, если бы число щук и окуней равнялось числу карасей)
21 : 3 = 7 (рыб) --- число карасей
7 + 2 = 9 (рыб) число щук
7 + 4 = 11 (рыб) число окуней.
ответ: 9 щук, 7 карасей, 11 окуней
Проверка: 7 + 9 + 11 = 27; 27 = 27
б) –123:41= -3
в) –147:(–7) = 21
г) 14,31:(2,7) =5,3
д) –86,2:(–0,1)=862
е) –51,34:(1,7)= -30,2