Расчет для одной, а не двух ламп приведен в таблице - в приложении.
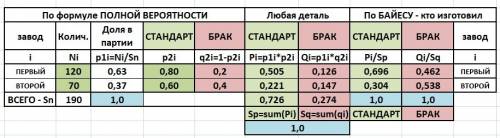
1) Находим вероятность Р1(i) -взять случайную из первой и второй партии: 0,63 и 0,37
2) Вероятность стандартной - P2(I) - дана: 0,8 и 0,6.
3) Берем "любую" деталь: произведение вероятностей: Р1 = 0,63*0,8 = 0,505 и Р2=0,221. Сложили и получили: вероятность стандартной - Sp = 0,726.
4) По формуле Байеса находим вероятность первого завода:
0.505 : 0.726 = 0.696 - на первом заводе и 0,304 - на втором.
Вот такой порядок решения для одной любой лампы.
7х/20 = 0,35х- набрал первый
13х/20 = 0,65х- осталось после первого
0,65х*0,6 = 0,39х - набрал второй
0,65х-0,39х = 0,26х - осталось после второго - и как раз эту часть набрал третий оператор
0,35х+0,39х = 0,74х - набрали первый и второй вместе
0,74х-0,26х = 0,48 х настолько первый и второй вместе набрали, чем третий. А это равно по условию 120 страниц.
Уравнение:
0,48х=120
х=120:0,48 = 250 (страниц) - в книге всего
Проверяем:
250* 0,35 = 87,5 стр. первый
(250-87,5) * 0,6 = 97,5 - второй
87,5+97,5 = 185 - 1 и 2 вместе
250-185=65 - третий набрал
185-65 = 120 стр. - настолько больше 1 и 2 больше чем третий.
Все сходится.
ответ: 87,5 стр., 97,5 стр., 65 стр.