Пусть x - количество верных ответов,
y - количество неверных ответов, x,y ∈ N
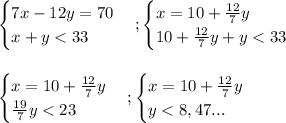
Так как x и y быть дробными не могут, y должен быть кратным 7.
По условию x,y ≥ 1, а по второму неравенству в системе y<8,47..., значит, y может быть равен только 7
y = 7
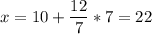 верных ответа дал ученик
верных ответа дал ученик
=================================
За каждый верный ответ ученик получает 7 очков. Так как 70 кратно 7, то как минимум ученик верно ответил на 70:7=10 вопросов.
Очки за остальные верные ответы были списаны по 12 очков за каждый неверный ответ. Числа 7 и 12 - взаимно простые. Наименьшее число, им кратное :
7*12 = 84 очка ученик заработал на верных ответах и потерял на неверных ответах.
84 : 7 = 12 ответов ученик дал верных, очки за которые потерял на неверных ответах.
Всего 10 + 12 = 22 верных ответа
Следующее число, кратное 7 и 12: 84*2 = 168.
168 : 7 = 24 верных ответа. 24 + 10 = 34 > 33. Такое решение не походит, так как не удовлетворяет условию вопросов викторины.
ответ: ученик дал 22 верных ответа.
а) 33 числа
б) 900 трёхзначных чисел; 450 чисел делятся на 2
в) 4 числа на 6 не делятся
г) 3 числа в каждой сотне делится на 26
Пошаговое объяснение:
а) Числа от 1 до 100, делящиеся на 3 без остатка: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99. Итого: 33 числа.
б) всего имеем трёхзначных чисел от 100 до 999, 999-99 = 900
нацело (без остатка) делятся на 2 чётные числа, т. е. половина того, что у нас есть: 900 / 2 = 450 чисел
в) 16,26,46,56, - 4 числа на 6 не делятся
6,36,66 - делятся на 6
г)26,52,78 - 3 числа в каждой сотне делится на 26