Пошаговое объяснение:
№ 1
2 sin 60 + cos 90 - tg 45
[ sin 60 = √3/2
tg 45 = 1 ]
2* √3/2 - 1 = √3 - 1
ответ 2)
№ 2
sin 120 = sin( 90+ 30) = cos 30 > 0
cos 195 = cos(180 + 15) = -cos 15 < 0
cos 359 = cos (-1) = cos 1 > 0
ответ: 4)
№ 3
6 cos^2 Pi/4 + tg^2 (-Pi/3) - ctg( - Pi/2)
[ cos Pi/4 = cos 45 = √2/2
cos^2 Pi/4 = 1/2
6 cos ^2 Pi/4 = 3
tg -Pi/3 = tg -60 = -tg 60 = -√3
tg^2 Pi/3 = 3
ctg( -Pi/2) = 0 ]
3+3-0=6
ответ: 3)
№ 4
(sin ( PI + a) * cos (Pi - a) ) / ctg(3*Pi/2 - a)
[ sin (Pi+a) = sin a
cos (Pi-a) = -cos a
ctg (3Pi/2 - a) = tg a = sin a/cos a ]
- sin a * cos a/ sin a /cos a = -cos^2 a
ответ: 1)
№ 5
sin a * cos a * ctg a - 1 = sin a * cos a * cos a/ sin a - 1 = cos^2 a -1 = - (1-cos^2 a) = -sin^2 a
ответ: 3)
№ 6
(sin^2 a - cos^2 a)/(sin a * cos a) = -cos 2 a / sin 2a/2 = -ctg 2a/2 = -0.5 ctg 2a
ответ: видимо, 4)
№ 7
2 sin 15 * cos 15 = sin 2*15 = sin 30 = 1/2
ответ: 4)
№ 8
cos 7Pi/4 = cos (-Pi/4) = cos Pi/4 = cos 45 = √2/2
ответ: 1)
№ 9
sin 105 = sin (60 + 45) = sin 60 * cos 45 + cos 60 *sin 45 = √3/2 * √2/2 + 1/2 * √2/2 = √6/4 + √2/4 = (√6+√2)/4
ответ: 2)
№ 10
[ sin = -3/5
tg 2 a = ? ]
cos^2 a = 1 - sin^2 a = 1 - 9/25 = 16/25 => cos a = 4/5. Но Pi < a < 3PI/2 => cos a = -4/5
tg 2a = sin 2a/cos2a
[ sin 2 a = 2sin a * cos a = 2 *12/25 = 24/25
cos 2 a = cos^2 a - sin^2 a = 16/25 - 9/25 = 7/25 ]
tg 2a = 24/25 / 7/25 = 24/7 = 3(3/7)
ответ: 4)
Пошаговое объяснение:
если на отрезке
y''(x) > 0, то функция вогнута на этом отрезке
y''(x) < 0, то функция выпукла на этом отрезке
найдем вторую производную от у(х)
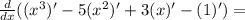
= 3(x²)' -10(x)' = 6x -10
теперь посмотрим, есть ли на отрезке [1;2] точки, где вторая производная меняет знак
6х-10 = 0 ⇒ х = 10/6
в этой точке вторая производная меняет знак, значит и функция меняет выпуклость
посмотрим знак возле этой точки х = 10/6; слева от нее y''(1) <0; справа от нее y'' (2) >0
таким образом
на [1; 10/6) функция выпукла
на (10/6; 2] функция вогнута
точка х = 10/6 - точка перегиба графика функции
9,3 - 2,7х = 3 2/7 + 1 3/14
9,3 - 2,7х = 4 1/2 = 4,5
-2,7х=4,5-9,3= -4,8
х= -4,8/(-2,7) = 1,78