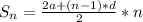
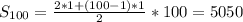
Два варианта ответов возможны :
1.
Яблок 88
Груш 2
Апельсинов 10
2.
Яблок 84
Груш 11
Апельсинов 5
Пошаговое объяснение:
Я -число яблок, Г - груш, А -апельсинов
0,5*Я+Г*3+А*5=100
Я+Г+А=100
Надо найти целочисленные решения.
Умножим первое уравнение на 2
Я+6Г+10А=200
Вычтем второе :
5Г+9А=100
ясно, что число апельсинов должно делиться на 5
Пусть оно равно 5*К
Г+9К=20
Целые решения Г=11 К=1 и Г=2 К=2
Если К=1 А=5 Груш 11 апельсинов 5
Яблок 100-16=84
Цена 42+33+25=100.
Значит такой вариант возможен.
Другое решение:
Если К=2 , то А=10 Г=2 Яблок 100-12=88
Цена 44+6+50=100
Значит такой вариант тоже возможн.
Разобьем их на пары и взвесим.
1. Пусть они весят поровну. Тогда рубин отложенный не фальшивый. А на одной чаше обязательно два фальшивых. На какой не знаем.
На любой из чаше заменяем один рубин (это второе взвешивание). Если ничего не изменилось - на второй чаше рубины фальшивые.
Если чаша стала легче или тяжелее, то на ней были фальшивые рубины.
2. Пусть другой случай : одна чаша сразу тяжелее другой.
Заменим один рубин на любой чаше на отложенный (второе взвешивание).
А) Пусть ситуация не изменилась. отложенный рубин был настоящий Заменили его тоже настоящим. Второй рубин на чаше был фальшивый. ТРЕБУЕТСЯ третье взвешивание, чтобы узнать какойиз двух рубинов на второй чаше фальшивый.
Б) Пусть весы уравновесились. Значит мы добавили фальшивый рубин.Второй тоже фальшивый.
Значит требуется в худшем случае ТРИ взвешивания.
Если они весят теперь поровну: