А) х+2х=6
3х=6
х=2
2 ребят нужно для мытья посуды
Б) 92/23=4 - т.е. посуды в 4 раза больше, чем той, которую можно вымыть за 15 минут
15*4=60 - для того того чтобы вымыть это количество посуды нужно 60 минут.
ответ: нельзя вымыть 92 прибора за 45 минут.
В) 14ч30м-15м-10м=14ч5м
14ч5м-13ч15м=50м
ответ: не успеют
Г)13ч15м+60м=14ч15м - закончат мыть посуду
14ч30м-10м=14ч20м - должны прийти в спортивный клуб, чтобы успеть переодеться
14ч20м-14ч15м=5м - на дорогу
750/5=150 м/мин.
ответ: со скоростью 150 м./мин. нужно идти, чтобы успеть на тренировку.
Надеюсь, логика понятна. С оформлением, к сожалению не могу.
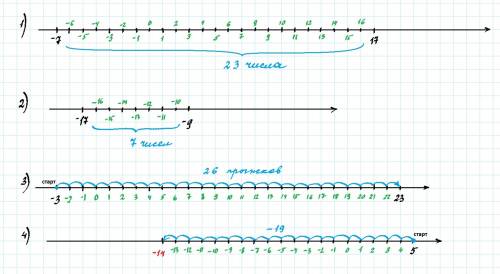
1) На координатном луче отмечаем точки (-7) и (17). Затем отмечаем все точки, лежащие между данными и соответствующие целым числам (смотри рис. 1). Считаем их количество. Получается 23.
Второй И еще из результата (24) вычитаем 1, т.к. одну крайнюю точку - (17) - учитывать не нужно..
24-1 = 23
ответ: 23
2) Чертим координатную прямую и отмечаем на ней точки (-17) и (-9). Затем отмечаем все точки между данными, соответствующие целым числам (см. рис. 2). Считаем их количество. Получается 9 чисел.
Либо можно сосчитать так: -9-(-17) = -9+17 = 8 – это количество чисел от (-17) до (-9), не считая (-17).
Убираем еще одно число, т.к. (-9) тоже не нужно учитывать.
8-1 = 7
ответ: 7
3) Кузнечик стартует в точке (-3), а в точке 23 останавливается.
Все целые числа он должен проходит по порядку. Ему необходимо прыгать только вправо. Тогда количество прыжков будет наименьшим. Если он сделает хоть один прыжок назад, это увеличит общее количество прыжков (см. рис. 3).
В этом случае от (-3) до 23 кузнечик сделает 23-(-3)=23+3=26 прыжков.
ответ: 26
4) Чертим числовую прямую. Отмечаем на ней точки, соответствующие целым числам. От точки (5) отсчитываем 19 целых чисел влево, т.к. нужно вычесть 19.
Оказываемся в точке (-14) (см. рис. 4)
ответ: -14
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении с поверхности небесного тела сможет:
v1 (круговая скорость) — стать спутником небесного тела (то есть вращаться по круговой орбите вокруг НТ на нулевой или пренебрежимо малой высоте относительно поверхности);v2 (параболическая скорость, скорость убегания) — преодолеть гравитационное притяжение небесного тела и уйти на бесконечность;v3 — покинуть звёздную систему, преодолев притяжение звезды;v4 — покинуть галактику.Третья и четвёртая космические скорости используются довольно редко. Вторая космическая скорость обычно определяется в предположении отсутствия каких-либо других небесных тел (например, для Луны скорость убегания равна 2,4 км/с, несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики). Еще реже в некоторых источниках встречается понятие "пятая космическая скорость". Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду[1]. Между первой и второй космическими скоростями существует простое соотношение:
Квадрат круговой скорости (первой космической скорости) с точностью до знака равен ньютоновскому потенциалу Φна поверхности небесного тела (при выборе нулевого потенциала на бесконечности):
где M — масса планеты, R — радиус небесного тела, G — гравитационная постоянная.
Квадрат скорости убегания (второй космической скорости) равен удвоенному ньютоновскому потенциалу, взятому с обратным знаком:
Первая и вторая космические скорости для различных объектов