Расстояние между двумя деревнями равное 40 км путешественик преодолел за 4 часа. часть пути он проехал за 1 час на велосипеде со средней скоростью 25 км.ч а оставшуюся часть пешком. с какой средней скоростью шёл путешественик?

👇

Увидеть ответ

Ответ:

nastyagrigorov

18.09.2020

1) 25*1=25 (км) - проехал на велосипеде

2) 40-25=15 (км пешком

3) 4-1=3 (ч.) - шёл пешком

4) 15:3=5 (км/ч)

ответ: путешественник шёл соскоростью 5 км/ч.

4,4(43 оценок)

Открыть все ответы

Ответ:

ггггггггггггжз

18.09.2020

ответ: 2

Значение выражений равно 2 вследствие доказанного равенства:

a = b = c

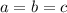
Пошаговое объяснение:

Запишем исходное равенство:

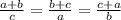
$\frac{a+b}{c} = \frac{b + c}{a} = \frac{c + a}{b}$

Прибавим + 1 к каждой части. Очевидно, что на равенство это никак не повлияет

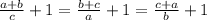
$\frac{a+b}{c} + 1 = \frac{b + c}{a} + 1= \frac{c + a}{b} + 1 \\$

Согласно условию, а, b, c - ненулевые, т.е знаменатель отличен от нуля у каждой представленной дроби.

Также для любых ненулевых a, b, c верно следующее:

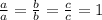
$\frac{a}{a} = \frac{b}{b} = \frac{c}{c} = 1$

Выразим единицу, прибавленную к каждой части соответствующей дробью:

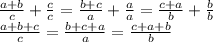
$\frac{a+b}{c} + \frac{c}{c} = \frac{b + c}{a} + \frac{a}{a} = \frac{c + a}{b} + \frac{b}{b} \\ \frac{a+b + c}{c} = \frac{ b + c + a}{a} = \frac{c + a + b}{b} \\$

Получаем дроби у которых

- в числителе одно и то же выражение

- в знаменателе а, b, c соответственно:

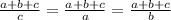
$\frac{a+b + c}{c} = \frac{a + b + c}{a} = \frac{a + b + c}{b}$

Раз числители равны - следовательно равны и знаменатели.

a = b = c

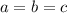
Для наглядности, пусть, a+b+c = x:

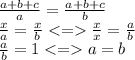
$\frac{a + b + c}{a} = \frac{a + b + c}{b} \\ \frac{x}{a} = \frac{x}{b} < = \frac{x}{x} = \frac{a}{b} \\ \frac{a}{b} = 1 < = a = b$

аналогично - для с.

А раз

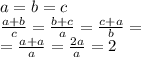
$a = b = c \\ \frac{a+b}{c} = \frac{b + c}{a} = \frac{c + a}{b} = \\ = \frac{a + a}{a} = \frac{2a}{a} = 2$

4,4(38 оценок)

Ответ:

eminka1

18.09.2020

Первый вопрос - ДА,
на гранях игрового кубика МОЖНО расположить очки с 14 до 19 так, чтобы
- на противоположных гранях была одинаковая сумма очков.
Всего 3 пары взаимно противоположных граней. Располагаем числа попарно так, чтобы сумма их была равна сумме первогого и последнего чисел
14 + 19
15 + 18
16 + 17
14 + 19
сумма во всех случаях будет равна
14 + 19 = 33

(Так что в ответе 33)

Второй вопрос - НЕТ,
на гранях игрового кубика НЕЛЬЗЯ расположить очки с 14 до 19 так, чтобы
на трёх гранях с общей вершиной была одинаковая сумма очков.
Пояснение: Любые соседние вершины (с общим ребром) из трех граней имеют по две общих. Пусть, это будут вершины А (сходятся грани a,b,c) и В сходятся грани a,b,d) Общими будут грани a, b.
Для равенства
а+b+c = a+b+d => c = d
Что невозможно.
Значит, невозможно разместить числа так, чтобы суммы трех граней при вершинах совпали.

(Так что в ответе 0 )

4,7(1 оценок)

Это интересно:

Дом-и-сад

31.05.2022

Как выжить при землетрясении: советы экспертов...

Кулинария-и-гостеприимство

30.04.2023

10 советов, как правильно пользоваться ножом для очистки овощей...

Питомцы-и-животные

07.04.2021

Незаменимая информация о травмах ACL у собак и методах их лечения, не требующих хирургического вмешательства...

Хобби-и-рукоделие