Если мы рассматриваем плоскость, то все просто.
1) Выбираем точку фигуры.
2) Проводим через это прямую перпендикулярную данной
3) Откладываем от данной прямой на продолжении начерченной отрезок равный по длине расстоянию от нашей точки, до данной прямой.
4) Сравниваем. Если конец отрезка попал на другую точку фигуры, то эти точки симметричны относительно данной прямой.
5) Если так проделать с каждой точкой фигуры (так чтобы точке с одной стороны соответствовала точка, и при том только одна, с другой) то мы получим симметричную фигуру относительно данной прямой
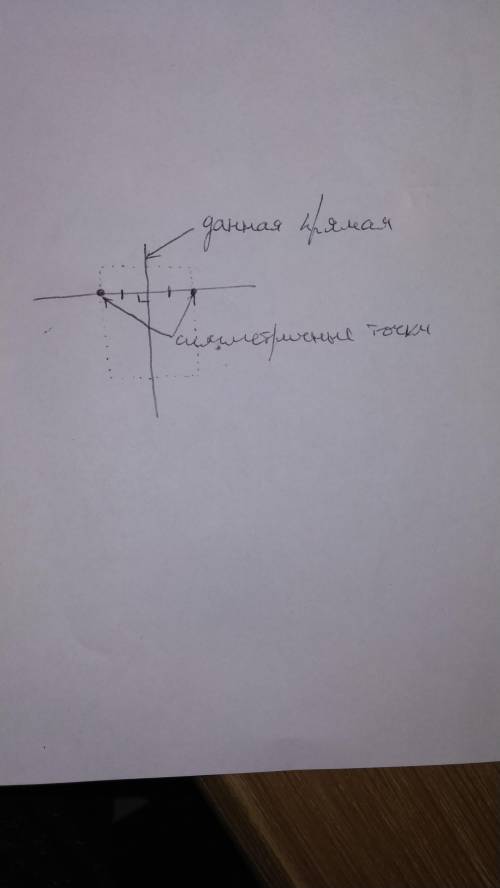
Пошаговое объяснение:
ну, судя по предлагаемым точкам у нас функция
![\displaystyle f(x) = 3 \sqrt [3]{x}](/tpl/images/4257/3722/63eb3.png)
рассмотрим уравнение касательной y = kx +b
здесь к - коэффициент наклона, он же tg угла наклона, он же производная в точке касания
нас интересует угол π/4. tg(π/4) = 1, значит надо найти точку, в которой значение производной будет =1
![\displaystyle f'(x) = \frac{1}{\sqrt[3]{x^2} }](/tpl/images/4257/3722/b2311.png)
![\displaystyle \frac{1}{\sqrt[3]{x^2} } =1 \quad \Rightarrow x_1=1; y_1=3; \quad x_2=-1;y_2= -3](/tpl/images/4257/3722/2aa7d.png)
вот мы получили две точки, в которых касательная будет наклонена к оси ох под углом π/4 M(-1; -3) и N(1; 3)
уравнения касательных
у нас есть уравнение у = кх +b
для нахождения уравнений двух касательных подставим поочередно в это уравнение координаты точек М и N
-3 = -1 + b ⇒ b = -2 ⇒ y₁ = x-2
3 = 1 +b ⇒ b = 2 ⇒ y₂ = x+2
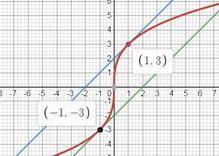
....