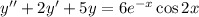
Общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного дифференциального уравнения, соответствующего данному неоднородному, и частного решения неоднородного дифференциального уравнения.
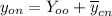
Составим однородное дифференциальное уравнение, соответствующее данному неоднородному:
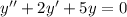
Составим характеристическое уравнение и решим его:
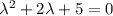
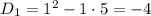
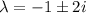
Общее решение однородного уравнения:
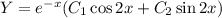
Запишем в общем виде частное решение данного неоднородного уравнения, учитывая, что в правой части стоит произведение экспоненты и на косинус, а также то, что степень экспоненты и выражение под знаком косинуса совпадают с соответствующими выражениями, полученными при решении однородного уравнения:
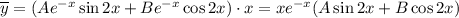
Находим первую производную:
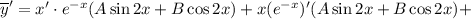
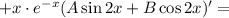
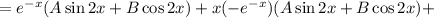
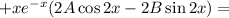
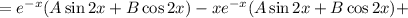
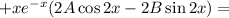
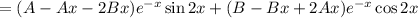
Находим вторую производную:
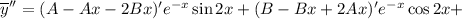
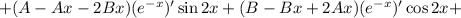
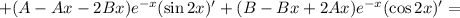
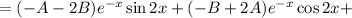

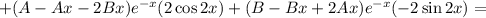
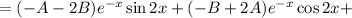
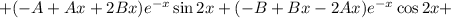
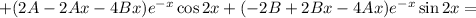
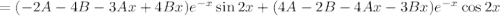
Подставляем в исходное уравнение:
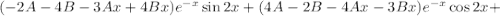
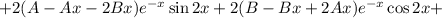
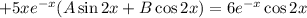
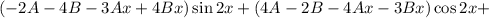
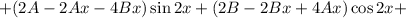
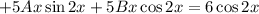
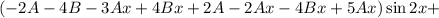
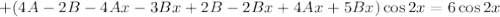
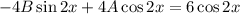
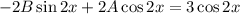
Условие равенства левой и правой частей:
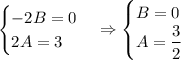
Частное решение данного неоднородного уравнения:
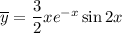
Общее решение данного неоднородного уравнения:
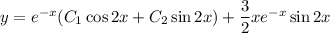
2)8% которой равны 56кг;4 кг= 56/0,08=700 4/0,08=50
3)15% которой равны 12см;2.7 см=12/0,15=12/0,15=80, 1,7/0,15=18
4)24% которой равны 9,6;42 т= 9,6/0,24=40,42/0,24=175
5)35% которой равны 21км;11,2= 21/0,35=60, 11,2/0,35=32
6)75% которой равны15ц; 90ц 15/0,75=20, 90/0,75=120