2
Пошаговое объяснение:
Раскройте скобки
(7+9)−1(11−7)=8
(7x+9){\color{#c92786}{-1(11x-7)}}=8(7x+9)−1(11x−7)=8
(7+9)−11+7=8
(7x+9){\color{#c92786}{-11x+7}}=8(7x+9)−11x+7=8
2
Раскройте скобки
(7+9)−11+7=8
(7x+9)-11x+7=8(7x+9)−11x+7=8
7+9−11+7=8
7x+9-11x+7=87x+9−11x+7=8
3
Сложите числа
7+9−11+7=8
7x+{\color{#c92786}{9}}-11x+{\color{#c92786}{7}}=87x+9−11x+7=8
7+16−11=8
7x+{\color{#c92786}{16}}-11x=87x+16−11x=8
4
Объедините подобные члены
7+16−11=8
{\color{#c92786}{7x}}+16{\color{#c92786}{-11x}}=87x+16−11x=8
−4+16=8
{\color{#c92786}{-4x}}+16=8−4x+16=8
5
Вычтите
16
1616
из обеих частей уравнения
−4+16=8
-4x+16=8−4x+16=8
−4+16−16=8−16
-4x+16{\color{#c92786}{-16}}=8{\color{#c92786}{-16}}−4x+16−16=8−16
6
Упростите
Вычтите числа
Вычтите числа
−4=−8
-4x=-8−4x=−8
7
Разделите обе части уравнения на один и тот же член
−4=−8
-4x=-8−4x=−8
−4−4=−8−4
\frac{-4x}{{\color{#c92786}{-4}}}=\frac{-8}{{\color{#c92786}{-4}}}−4−4x=−4−8
8
Упростите
Сократите числитель и знаменатель
Разделите числа
=2
Пошаговое объяснение:
1.
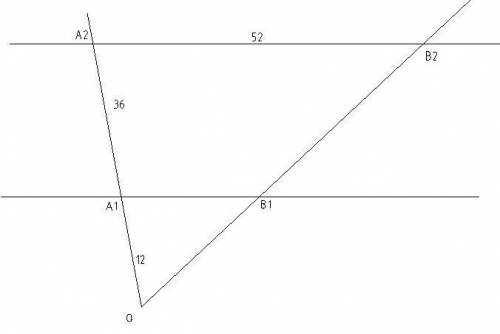
А1В1 и A2B2 отрезки прямых, полученных при пересечении двух параллельных плоскостей третьей плоскостью - плоскостью двух лучей с общим началом в точке O по условию, значит А1В1 II A2B2, значит углы А1В1О = А2В2О и ОА1В1 = ОА2В2, угол О - общий.
следовательно треугольники ОА1В1 и ОА2В2 подобны
из соотношения ОА2:ОА1 = 36+12:12 получаем коэффициент подобия 4
следовательно А1В1 подобна А2В2 с коэффициентом 4
Значит А1В1 = А2В2 : 4 = 13
2.
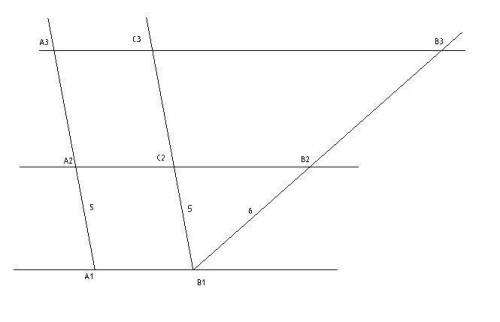
Проведем прямую параллельную А1А3 через точку В1 - имеем параллелограммы А1А2С2В1 и А2А3С3С2 из свойств которых следуют равенства А1А2=В1С2, А2А3=С2С3.
аналогично 1 задаче имеем подобные треугольники В1С2В2 и В1С2С3
Из отношения В1В2:В2В3=2:5 найдем что В2В3 = 6:2*5 = 15
В1В3=В1В2+В2В3=6+15 = 21
Значит В1С2:С2С3 = 2:5
Аналогично найдем С2С3 = В1С2 : 2 * 5 = 12.5
Откуда А1А3=В1С3=5+12.5=17.5