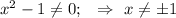
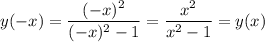
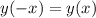Математика: Найди значение выражения -3*(9х-5y)-7*(2х-3y), если х= -0,3, y=0,6

Найди значение выражения -3(9х-5y)-7(2х-3y), если х= -0,3, y=0,6

👇

Увидеть ответ

Ответ:

MrCriMa

15.03.2022

-3*(9х-5y)-7*(2х-3y)=-27x+15y-14x+21y=36y-41x
при x=-0,3 y=0,6 36*0,6-41*(-0,3)=21,6+1,23=22,83

4,4(92 оценок)

Открыть все ответы

Ответ:

HermioneGranger19

15.03.2022

1. Область определения функции: $x^2-1\ne 0;\,\,\,\,\, \Rightarrow\,\, x\ne \pm 1$
$D(f)=(-\infty;-1)\cup(-1;1)\cup(1;+\infty)$
2. Исследуем на четность.
$y(-x)= \dfrac{(-x)^2}{(-x)^2-1} = \dfrac{x^2}{x^2-1}=y(x)$
Поскольку y(-x)=y(x)

, то эта функция четная.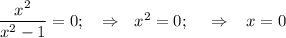

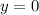
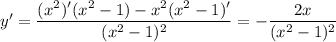
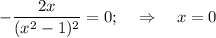
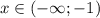3. Функция не периодическая.
4. Точки пересечения с осью Ох и Оу.
4.1. С осью Ох (если у=0)
$\dfrac{x^2}{x^2-1} =0;\,\,\,\,\,\,\Rightarrow\,\,\,\, x^2=0;\,\,\,\,\,\,\,\, \Rightarrow\,\,\,\,\, x=0$
4.2. C осью Оу (если х = 0)
y=0

5. Точки экстремумы и монотонность функции:
$y'= \dfrac{(x^2)'(x^2-1)-x^2(x^2-1)'}{(x^2-1)^2} =- \dfrac{2x}{(x^2-1)^2}$
Приравниваем производную функции к нулю:
$- \dfrac{2x}{(x^2-1)^2}=0;\,\,\,\,\,\,\, \Rightarrow\,\,\,\,\,\, x=0$

__+___(-1)__+___(0)___-___(1)___-____
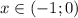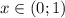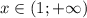
Функция возрастает на промежутке $x \in (-\infty;-1)$ и $x \in (-1;0)$ , а убывает на промежутке $x \in (0;1)$ и $x\in (1;+\infty)$
В окрестности точки x=0

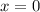производная функции меняет знак с (+) на (-), следовательно, точка x=0

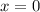- точка максимума.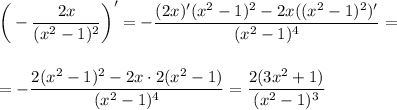

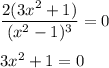
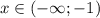5. Точки перегиба.
Вычисляем вторую производную функции:
$\bigg(- \dfrac{2x}{(x^2-1)^2}\bigg)'=- \dfrac{(2x)'(x^2-1)^2-2x((x^2-1)^2)'}{(x^2-1)^4} =\\ \\ \\ =- \dfrac{2(x^2-1)^2-2x\cdot 2(x^2-1)}{(x^2-1)^4} = \dfrac{2(3x^2+1)}{(x^2-1)^3}$

Приравниваем к нулю
$\dfrac{2(3x^2+1)}{(x^2-1)^3} =0\\ \\ 3x^2+1=0$
Уравнение решений не имеет, так как левая часть уравнения принимает только положительные значения.

___+____(-1)___-____(1)___+___
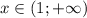На промежутке $x \in (-\infty;-1)$ и $x \in (1;+\infty)$ функция вогнута, а на промежутке 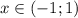$x \in (-1;1)$ функция выпукла.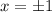

Вертикальные асимптоты: $x=\pm1$

Горизонтальные асимптоты:
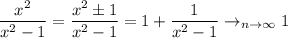
$\displaystyle \dfrac{x^2}{x^2-1} = \dfrac{x^2\pm1}{x^2-1} =1+ \frac{1}{x^2-1} \to_{n\to \infty}1$
y=1

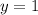- горизонтальная асимтота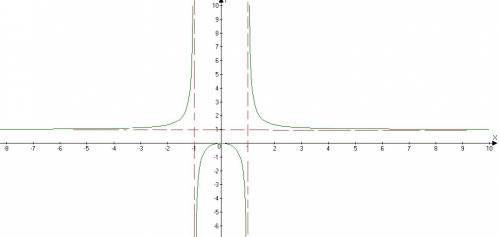

Наклонных асимптот нет.

Исследование функции y=(x^2)/(x^2-1)

4,4(98 оценок)

Ответ:

kira309

15.03.2022

Копьё чжида оснащалось различными наконечниками. Были широкие плоские (листовидные), гранёные узкие и ножевидные. Многие источники той эпохи описывали вариант монгольского копья с крюком под наконечником, который облегчал стаскивание противника с седла. Это был упрощённый монгольский вариант чжурчжэньского копья, у которого к наконечнику на шарнире монтировалось лезвие, поджимаемое назад. При возвратном рывке это лезвие фиксировалось поперечно древку и не только выдёргивало врага из седла, но и наносило ужасающие раны.Древковые оружия упокоения смертных весьма сложных форм. Самые простые из оных это боевые вилы, вилки да трезубцы.Мечи, сабли и палаши,лук. И всё же самым распространённым клинком была сабля. Её изогнутый клинок был лучшим для убивания вражьих сил.Очень ходовым оружием были боевые ножи и топоры. В росте такой ножичек достигал 40 см. Обычно отделка ножа была сходна декору длинных клинков.

4,6(95 оценок)

Это интересно:

Компьютеры-и-электроника

13.11.2020

Как вычислить пропускную способность?...

Компьютеры-и-электроника

30.08.2022

Как найти железо в игре Minecraft: советы для начинающих игроков...

Компьютеры-и-электроника

27.02.2020

Как добавить звук в Google Презентацию...

Финансы-и-бизнес