Пошаговое объяснение:
1) Цилиндр
R=6дм - радиус цилиндра
h=15dm -высота цилиндра
Sцилиндра=2πR(R+h)
Sцилиндра=2π*6(6+15)=12*21π=252π дм²
Sцилиндра=252π=252*3,14=791,28 дм²
2)прямоугольный параллелепипед со сторонами 10×8×10
а=10 дм -длина
в=8 дм -ширина
с=10дм -высота
S=2ас+2вс+2ва
S(10×8×10)=2*10*10+2*8*10+2*8*10=
=200+160+160=520 дм²
3)прямоугольный параллелепипед со сторонами 14×6×10
а=14 дм -длина
в=6дм -ширина
с=10дм -высота
S=2ac+2вс+2ва
S(14×6×10)=2*14*10+2*14*6+2*10*6=
280+168+120=568 дм²
Смотрим на площади трёх фигур
Sцилиндр=791,28дм²
S(10×8×10)=520дм²
S(14×6×10)=568дм²
Самая маленькая площадь у фигуры со сторонами 10×8×10, на нее использовалось меньше всего стекла
ответ: фигура на рисунке В.
см. рис.
Пошаговое объяснение:
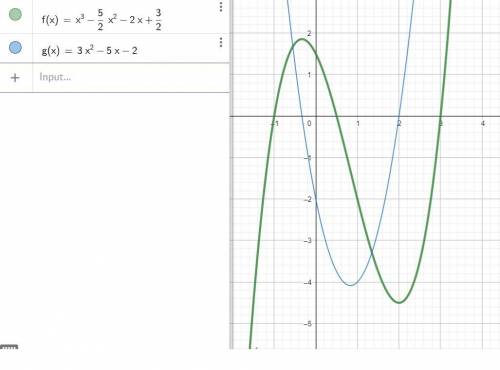
кубическая парабола, снизу-вверх.
Взять производную,
исследовать f'(x) на f'(x) < 0, f'(x) > 0
определить экстремумы.
f'(x) = 3x² - 5x - 2
f'(x) = 0 при
3x² - 5x - 2 = 0
D = 25 - 4 * 3 * (-2) = 49 - 7²
x1 = (5-7) / 6 = -1/3
x2 = (5+7) / 6 = 2
f'(x) = 3x² - 5x - 2 (роги вверх => меньше нуля - между корнями)
f'(x) < 0 при x ∈ (-1/3; 2) => f(x) убывает
f'(x) > 0 при x ∈ (-∞; -1/3) ∪ (2; +∞) => f(x) возрастает
х1 - точка максимума
х2 -точка минимума
f(-1/3) = (-1/27) - (5/2)*1/9 - 2*(-1/3) + 3/2 = -1/27 - 5/18 + 2/3 + 3/2 =
= -1/27 + (-5 + 12 +27)/18 = -1/(9*3) + 34/(9*2) = (-2+102) / (9*3*2) =
= 100/54 = 1+46/54 : (почти 2)
f(2) = 8 - 10 - 4 + 3/2 = -4,5
f(0) = 3/2
дальше строим график, если руками - то считаем точки и соединяем плавной кривой.
примерно представив график можно проверить нули функции:
f(-1) = 0
f(1/2) = 0
f(3) = 0
день
первый день
16,9+11,1=28