Начертите прямоугольник.проведите прямую,которая разобьёт его на две равных прямоугольника.сколько разных решений вы нашли с фоткой бы не отказался

👇

Ответ:

Оажлцоа

30.09.2021

Прямоугольник и на два прямоугольника - готово в приложении.
Два варианта.
Начертите прямоугольник.проведите прямую,которая разобьёт его на две равных прямоугольника.сколько р

Начертите прямоугольник.проведите прямую,которая разобьёт его на две равных прямоугольника.сколько р

4,5(83 оценок)

Открыть все ответы

Ответ:

Msскрытность

30.09.2021

Пошаговое объяснение:

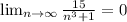$\lim_{n \to \infty} \frac{15}{n^3+1}=0$ . Докажем это.

По определению предела, для всякого положительного ε найдется номер N, что для всех номеров n, бОльших N, верно, что 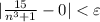$| \frac{15}{n^3+1}-0|< \varepsilon$ .

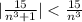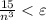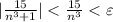Заметим, что $| \frac{15}{n^3+1}|< \frac{15}{n^3}$ для всякого натурального n. Тогда, если $\frac{15}{n^3}< \varepsilon$ , или (решая неравенство относительно n) $n \sqrt[3]{\frac{15}{\varepsilon}}$ , то, взяв в качестве N целую часть числа $\sqrt[3]{\frac{15}{\varepsilon}}$ , получим, что $| \frac{15}{n^3+1}|< \frac{15}{n^3} < \varepsilon$ . 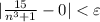Резюмируя: научились для всякого положительного ε находить номер N (в качестве N можно взять целую часть числа $\sqrt[3]{\frac{15}{\varepsilon}}$ ), что для всех номеров n, бОльших N, выполняется неравенство $| \frac{15}{n^3+1}-0|< \varepsilon$ . А это и значит, что предел равен нулю.

Интуитивно это можно объяснить так: увеличивая номер n, получаем все меньшее и меньшее число, причем оно всегда больше нуля, но его можно сделать очень маленьким.

Аналогично, докажем, что 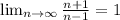$\lim_{n \to \infty} \frac{n+1}{n-1}=1$

По определению предела, для всякого положительного ε найдется номер N, что для всех номеров n, бОльших N, верно, что 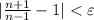$| \frac{n+1}{n-1}-1|< \varepsilon$ .

Заметим, что 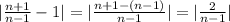$|\frac{n+1}{n-1}-1|=|\frac{n+1-(n-1)}{n-1}|=|\frac{2}{n-1}|$ . Тогда, если 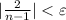$|\frac{2}{n-1}|< \varepsilon$ , или (решая неравенство относительно n) 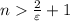$n \frac{2}{\varepsilon}+1$ , то, взяв в качестве N целую часть числа 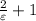$\frac{2}{\varepsilon}+1$ , получим, что 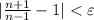$| \frac{n+1}{n-1}-1|< \varepsilon$ . Резюмируя: научились для всякого положительного ε находить номер N (в качестве N можно взять целую часть числа 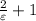$\frac{2}{\varepsilon}+1$ ), что для всех номеров n, бОльших N, выполняется неравенство 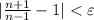$| \frac{n+1}{n-1}-1|< \varepsilon$ . А это и значит, что предел равен единице.

4,7(72 оценок)

Ответ:

Snowghost

30.09.2021

Методом подбора, раз драконы 3-х головые, и всего голов 31, надо найти сколько драконов может поместиться в числе до 31 .
10,9.8,7,6 - не подходит потому что количество ног на количество драконов не деоится без остатка, а вот 5 подходит
5драконов * 3 головы каждому = 15 голов уйдёт на драконов
всего голов 31 - 15 = 16 остаётся одноногим Тринадцатичетырёхножкам так как они одноногие то и ног на них уйдёт 16
общее число ног 286 - 16 = 270 ног остаётся нашим драконом, учитывая что их 5
270 : 5 = 54 каждому достаётся по 54 ноги

ответ у каждого трёхголового дракона 54 ноги.

4,4(78 оценок)

Это интересно:

Здоровье

05.02.2021

Как избавиться от узлов в мышцах: причины, симптомы и методы лечения...

Семейная-жизнь

23.06.2022

Как избежать рвоты беременных...

27.02.2021

Как изменить всю свою личность: советы от психологов...

Питомцы-и-животные

17.04.2023