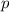и 
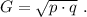
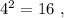а произведение двух самых больших равно 
»
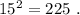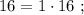
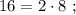
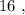т.е.: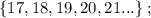 
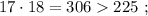
каждое – будет, очевидно, больше чем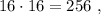 
т.е. больше 
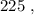а значит, при выборе минимальных чисел в виде 
и – подобрать остальные числа невозможно.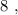
т.е.: 
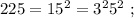
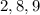и 
и 
и 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы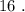 
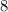и никаких натуральных чисел нет. и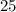 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы 
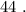
x^n - y^n = (x - y)(x^(n-1) + x^(n-2) * y + x^(n-3) * y^2 + + x * y^(n-2) + y^(n-1))
Из нее следует, что a^(2k) - 1 разлагается на множители:
a^(2k) - 1 = (a^2)^k - 1 = (a^2 -1)((a^2)^(k-1) + (a^2)^(k-2) + + (a^2)^ + 1).
Отсюда следует, что a^(2k) - 1 делится на a^2 - 1.