y=kx+b -прямая. Расположение зависит от коэффициента при x(сейчас это k). Если k положительный, то график проходит в 1 и 3 плоскостях, а если нет- во 2 и 4. Строится табличным парабола. Число при x так же отвечает за вид графика. Если a положительное, то ветви параболы направленны вверх, а если отрыцательное- вниз. Чтобы построить параболу нужно сначала найдем ее x вершину: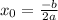 
, затем эту X вершину подставляем в 
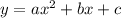и находим Y вершину. Далее нужно найти точки пересечения осей графика. Для этого обозначаем X и, затем, Y за 0 и находим точки пересечения осей. Параболу можно строить и табличным Если при X степень нечетная( не квадрат, а куб, нарпимер), тогда парабола имеет другой вид: одна ее ветка направлена вверх, другая- вниз.
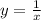-гипербола (X- обязательно знаменатель!). Находится или в 1 и 3 плоскосли, или во 2 и 4. В этой функции X не может быть 0, поэтому гипербола никогда не пересечет ни ось абцисс, ни ось ординат. Строится табличным одна ветка параболы. X не может быть отрицательным. Строится табличным прямые. Имеет форму галочки. Одна прямая симетрична другой. X может быть как больше 0, так и меньше 0. Направление веток определяет коэффициент при модуле(-|X| или |X|).
5) z = 0 - (-6), z = 0 + 6, z = 6
6) z/5 = -7 -3, z/5 = -7 + (-3), z/5 = -10, z = -10 · 5, z = -50
7) a = 2,8 - (-2,8), a = 2,8 + 2,8, a = 5,6
8) n = -4,5 + 1,4, n = -3,1; 1 2/5 = 1,4
9) x + 3 = 12 : 2, x + 3 = 6, х = 6 - 3, х = 3
10) -2(1 - у) = -8 - 3, -2(1 - у) = -11, 1 - у = -11 : 2, 1 - у = -5,5, у = 1 - (-5,5), у = 6,5