объем параллелепипеда V=30 (ед.из)
Пошаговое объяснение:
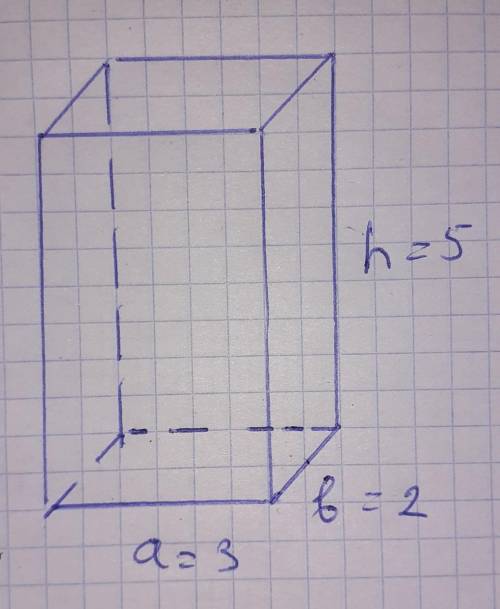
Площадь поверхности прямоугольного параллелепипеда равна 62. Два его ребра, выходящие из одной вершины, равны 2 и 3. Найдите объем параллелепипеда.
Sв.пов=62 (ед. из)
допустим что длина основания равна
а=3
ширина основания
в=2
надо найти высоту h . потом и объем параллелепипеда.
Площадь всей поверхности параллелепипеда это сумма площадей всех 6 граней, двух основании ( верхнего и нижнего) и четырёх боковых граней.
Sв.п= 2×Sосн + Sбок, где
Sосн=а×b
Sбок=P×h,
P периметр основания Р=2а+2b
P=2×3+2×2=6+4=10
площадь основания
Sосн=а×b=3×2=6
площадь боковой поверхности
Sбок=Sв.п-2×Sосн=62 - 2×6=50
высота параллелепипеда
h=Sбок/P=50/10=5
объем параллелепипеда
V=abh=3×2×5=30 (ед.из)
14 целых 7\24 -8 целых 1\16 - 5 целых 1\6=1 7/48
1) 14 14/48-8 3/48-5 4/48=1 7/48 (привели все к одному знаменателю)
22 целых 1\3 -(10 целых 7\12 + 9 целых 11\20)=1/5
20 20/60-(10 35/60+9 33/60)=20 20/60-19 68/60=20 20/60-20 8/60=12/60=1/5
10 целых - (5 целых 7\8 + 3 целых 5\12)=17/24
10-(5 21/24+3 10/24)=10-8 31/24=10-9 7/24=9 24/24-9 7/24=17/24
№2
№3
а) (9 1\4-8 2\3)*1 5\7+(4 2\9-2 5\6):1 1\9 =2 1/4
1) 9 1/4-8 2/3=9 3/12-8 8/12=8 15/12-8 8/12=7/12
2) 4 2/9-2 5/6=4 4/18-2 15/18=3 22/18-2 15/18=1 7/18
3) 7/12*1 5/7=7/12*12/7=1
4) 1 7/18:1 1/9=25/18:10/9=25/18*9/10=5/4=1 1/4
5) 1+1 1/4=2 1/4
б)2 3\11*7\9+ 6 8\11: 1 2\7 -1 1\8=5 7/8
1) представим деление в виде умножения: 6 8/11:1 2/7=6 8/11:9/7=6 8/11*7/9
2) вынесем общий множитель за скобки:
2 3\11*7\9+ 6 8\11*7/9=7/9*(2 3/11+6 8/11)=7/9*8 11/11=7/9*9=7
3) 7-1 1/8=6 8/8-1 1/8=5 7/8