Запишем формулу: P=m/n, где m – число исходов, благоприятствующих осуществлению события X, а n – число всех равновозможных элементарных исходов.
Для начала определим вероятность выпадения орла или решки при одном броске. Выпадает всегда 1 результат, а всего исходов 2. Значит, вероятность выпадения орла или решки = 1/2. Но бросков мы делаем 2, а значит, количество исходов возводится в квадрат и теперь равно 1 / 2 × 2 = 1/4. В последующем мы будем домножать числитель на количество удовлетворяющих нас исходов.
Значение "Решка выпала хотя бы 1 раз" верно при следующих результатах:
1) решка и орёл
2) орёл и решка
3) решка и решка
Как видим, количество удовлетворяющих нас результатов =3, а значит, в двух бросках решка выпадает хотя бы один раз с вероятностью 1 × 3 / 4 = 3/4 = 0.75 = 75%
В первый раз выпал орёл при следующих результатах:
1) орёл и решка
2) орёл и орёл
Как видим, количество удовлетворяющих нас результатов =2, а значит, в двух бросках орёл выпадет первым с вероятностью 1 × 2 / 4 = 2/4 = 1/2 = 0.5 = 50%
ответ: 75%, 50%.
Пошаговое объяснение:
Объясню на примере 2965 х 72
Сначала цифру 2 умножаем поочерёдно на все цифры верхней строчки :
2 х 5 = 10 ( 0 пишем, 1 в уме)
2 х 6 = 12 ( прибавляем 1, что был в уме = 13.... 3 пишем, 1 опять в уме)
2 х 9 = 18 ( прибавляем 1, что был в уме = 19... 9 пишем, 1 опять в уме)
2 х 2 = 4 ( прибавляем 1, что был в уме и пишем 5)
И так далее со вторым числом.
Но! Все последующие расчёты мы записываем со сдвигом на одну цифру, иначе не сойдется.
Если в множителе есть ноль, то мы не пишем нули в строчке, а просто сдвигаем строчку ещё на одну цифру!
Как на картинке. Нули можно не писать, но тогда нижняя строчка сдвинется на 2 цифры влево
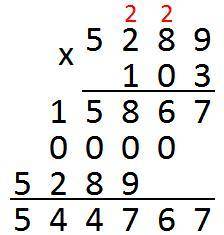
42:2*100=21*100=2100
27:10*100=270
35:5*100=7*100=700