 и
и 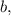 то ничего не изменится, всё будет работать как прежде.
то ничего не изменится, всё будет работать как прежде.
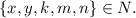
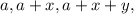 чтобы
чтобы![( [ a + 1 ] + x + y ) | ( 2a+x ) ,](/tpl/images/0497/6250/3dbb9.png)
![( [ a + 1 ] + x ) | ( 2a+x+y )](/tpl/images/0497/6250/bcfc5.png) и
и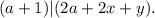
![k ( [ a + 1 ] + x + y ) = 2a + x](/tpl/images/0497/6250/3a31a.png) ;
;![(k-1) x + ky = 2a - k [ a + 1 ]](/tpl/images/0497/6250/d1c79.png) ;
;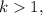 правая часть отрицательная, а левая положительна, что не возможно.
правая часть отрицательная, а левая положительна, что не возможно.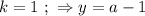 ;
;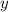 его значение
его значение 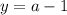 и будем искать такие комбинации
и будем искать такие комбинации 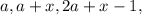 чтобы:
чтобы: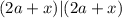 – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 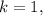
![( [ a + 1 ] + x ) | ( 3a+x-1 )](/tpl/images/0497/6250/b244e.png) и
и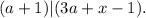
![m ( [ a + 1 ] + x ) = 3a+x-1](/tpl/images/0497/6250/c1228.png) ;
;![(m-1) x = 3a - 1 - m [ a + 1 ]](/tpl/images/0497/6250/be1b0.png) ;
;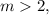 правая часть отрицательная, а левая положительна, что не возможно.
правая часть отрицательная, а левая положительна, что не возможно.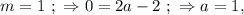 но это не подходит по условию.
но это не подходит по условию.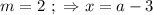 ;
; его значение
его значение 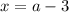 и будем искать такие комбинации
и будем искать такие комбинации 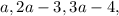 чтобы:
чтобы:![( 3 [ a - 1 ] ) | ( 3 [ a - 1 ] )](/tpl/images/0497/6250/de3e6.png) – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 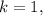
![( 2 [ a - 1 ] ) | ( 4 [ a - 1 ] )](/tpl/images/0497/6250/02549.png) – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 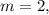
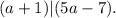
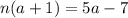 ;
;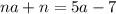 ;
; ;
;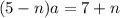 ;
;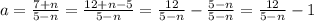 ;
;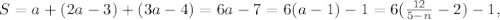
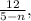 т.е. при
т.е. при 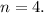
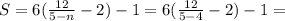
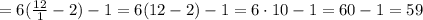 ;
;В жизни часто приходится встречаться с различными совокупностями объектов, объединёнными в одно целое по некоторому признаку. Для обозначения этих совокупностей используются различные слова. Например, говорят: «стадо коров», «букет цветов», «команда футболистов» и т. д.
В математике в целях единообразия для обозначения совокупностей употребляется единый термин — множество. Например, говорят: множество чётных чисел, множество двузначных чисел, множество правильных дробей со знаменателем 5.
Термин «множество» употребляется и тогда, когда речь идёт о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек координатной плоскости, о множестве прямых, проходящих через данную точку.
Объекты или предметы, составляющие множество, называют элементами множества. Например, число 89 — элемент мнoжества двузначных чисел; точка В — элемент мнoжества вершин многоугольника ABCDE.
Множeства бывают конечные и бесконечные. Например, множество двузначных чисел — конечное множество (оно содержит 90 элементов), а множество чётных чисел — бесконечное множество.
Пошаговое объяснение:
в гараже 340 машин.москвичи составляют 45%от жигули а запорожец ,-5/9 от москвичей сколько автомашин каждого вида
х(м.)-жигули0,45х(м.)-москвичи
0,45х*5/9=0,25х(м.)-запорожцев
всего 340 машин, получается:
х+0,45х+0,25х=340
1,7х=340
х=340/1,7
х=200(м.)-жигули
200*0,45=90(м.)-москвичи
90*5/9=50(м.)-запорожцев
пусть жигулей х
тогда, 0,45 х - москвичей 5/9* 0,45 х= 0,25х - запорожцев х+0,45х+0,25х=340 1,7х=340 х=200 200 жигулей 0,45*200=90 москвичей 340-200-90=50 запоржцев