Задача. Подбрасывается 12-гранный кубик, на гранях которого написаны числа от 1 до 12. Вероятность выпадения i-ой грани пропорциональна (с одним и тем же коэффициентом пропорциональности) числу, написанному на этой грани, то есть,
P(выпало число i) = k * i
Вероятность выпадения k,2k,3k,...,12k. Сумма вероятностей k + 2k + 3k + ... +12k = 78к должна равняться 1, т.е. 78k = 1 откуда k = 1/78
Число очков большее чем 6 это 7, 8, 9, 10, 11, 12.
Вероятность того, что выпало число очков, большее 6, равна
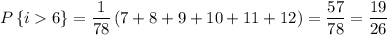
ответ: k = 1/78 и P = 19/26
ответ:
вероятность попадания р1 = 0,7 => вероятность промаха р2 = 0,3.
cобытия "попадание" или "промах"при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей.
тогда вероятность р того, что он из 4 раз первый раз попал, а последние 3 раза промахнулся равна:
p = р1 * р2 * р2 * р2 = 0,7 * 0,3 * 0,3 * 0,3 = 0,7 * 0, 027 = 0,0189
ответ: 0,0189.