сейчас решить не могу.
по этому примеру решай
Пошаговое объяснение:
Чтобы разобраться с решением задачи, необходимо, её внимательно прочитать и переформулировать условие. Можно выполнить чертёж (молоко, налитое в каждый бидон, изобразить отрезком).
1-ый бидон - 4 11/20 л, (начертите отрезок).
2-ой бидон - ? л, на 1 3/5 л б., чем в 1-ый (изобразите отрезком большей длины, чем 1-ый).
3-ий бидон - ? л, на 17/20 л м., чем в 1- (изобразите отрезком меньшей длины, чем 1-ый).
Всего - ? л. (Либо вопрос после объединяющей скобки).
4 11/20 + 1 3/5 = 6 1/20 л - 2-ой бидон.
4 11/20 - 17/20 = 3 14/20 л 3-ий бидон.
4 11/20 + 6 1/20 + 3 14/20 = 14 6/20 л - в 3-х бидонах.
ответ: 14 3/10 литра молока в трёх бидонах.
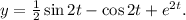
Пошаговое объяснение:
Имеем дело с неоднородным линейным уравнением с постоянными коэффициентами. Стандартный прием: искомое решение представляется в виде суммы решения однородного уравнения и частного решения неоднородного: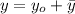 
.
Однородное уравнение: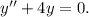 
Характеристическое уравнение имеет следующий вид: 
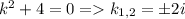. Тогда решение однородного уравнение можно записать в виде: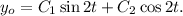 
Так как в правой части исходного уравнения перед экспонентой стоит многочлен нулевой степени, а коэффициент в показателе экспоненты не совпадает с каким-либо корнем характеристического уравнения, то частное решение можно искать в виде: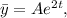 
подставим его в исходное уравнение и найдем коэффициент 
:
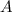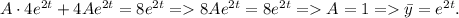
Значит, общее решение исходного уравнения есть
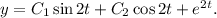Осталось определить коэффициенты для данной задачи Коши:
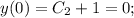
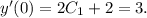
Решая каждое из этих уравнений, находим: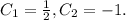 
В итоге, получаем ответ:
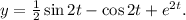
100-5=95 (%) - влаги в 1 710 т травы.
составим пропорцию:
1 710 т - 95%
х т - 100%
(т) - травы осталось на второй день.
100-10=90 (%) - влаги в 1 800 т травы.
составим пропорцию:
1 800 т - 90%
х т - 100%
(т) - травы было скошено.
ответ: было скошено 2 000 тонны травы.