Пошаговое объяснение:
Обєм призми: V=S(основи)*h
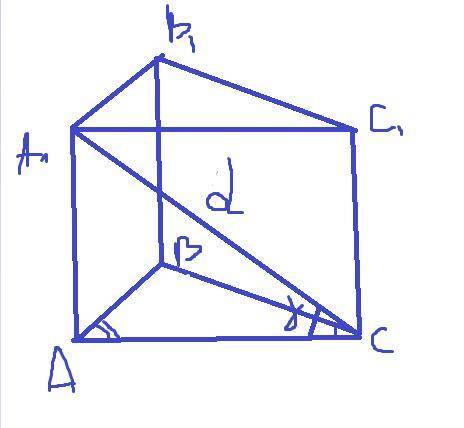
Бічні грані прямої призми - прямокутники.
За означення sin знайдемо висоту призми.
h=d*sin(гама).
За означення cos знайдемо одну зі сторін трикутника який лежить в основі прямої призми.
AC=d*cos(гама).
Також можна знайти АВ і АС за теоремою Піфагора
Так як BB1-висота призми,яка нахилена до основи призми під кутом 90 градусів.
BC^2=d^2-d^2*sin^2(гама)=d*Sqrt(1-sin^2(гама))=d*cos(гама)
AB дорівнює теж d*cos(гама).
Знайдемо за формулою Герона площу трикутника АВС
S=Sqrt(p*(p-a)*(p-b)*(p-c)
p=3/2cos(гама)
S=Sqrt(3/2cos(гама)*(3/2cos(гама)-cos(гама))*(3/2cos(гама)-cos(гама))*(3/2cos(гама)-cos(гама))=Sqrt(3/2cos(гама)*(cos(гама)/2)*(cos(гама)/2)*(cos(гама)/2)=Sqrt(3cos^4(гама)/16))=Sqrt(3)*cos^2/4
V=Sqrt(3)*cos^2/4*d*sin(гама).
ответ: Первому 3 целых 4/7 дня; второму 4/7 дня.
Пошаговое объяснение: Условие немного сумбурное, (первая часть задачи повторяется два раза), но суть ясна.
Пусть вся работа 1 (единица), х дней, время за которое второй рабочий выполнит всю работу самостоятельно, тогда время за которое первый рабочий выполнит всю работу, будет х+3 дней, соответственно производительность первого рабочего 1/(х+3) раб/день, а второго рабочего 1/х раб/день. 1,5 дня = 3/2 дня. По условию задачи составим уравнение:
(1-(1/(х+3))*(3/2))÷((1/х)+1/(х+3))=2/7
((2х+3)/(2х+6))÷((2х+3)/(х²+3х))=2/7
(х²+3х)/(2х+6)=2/7
7х²+17х-12=0
D=625
х₁=-3 (дня) не подходит, т.к. время не может быть отрицательным.
х₂=4/7 (дня) нужно второму рабочему, чтобы выполнить всю работу самостоятельно.
(4/7)+3=(3 4/7) (дня). 3 целых 4/7 дня нужно второму рабочему, чтобы выполнить всю работу самостоятельно.
С запятыми,ну что-то типо того)