y=x^2-6x+9
y=3x-9
Первая линия - график кв. параболы касающейся оси х в точке 3, т.к.
D=36-36=0
x=6/2=3
Вторая линия - прямая, пересекающая ось Х в точке 3, тк.
3х-9=0 x=3 и ось у в точке -9, т.к. у=3*0-9=-9
Точки пересечения двух этих линий вычисляются так:
приравниваем оба уравнения
x^2-6x+9=3x-9
решаем относительно х:
x^2-6x+9-3x+9=0
x^2-9x+18=0
D=81-18*4=9
x1=(9+3)/2=6
x2=(9-3)/2=3
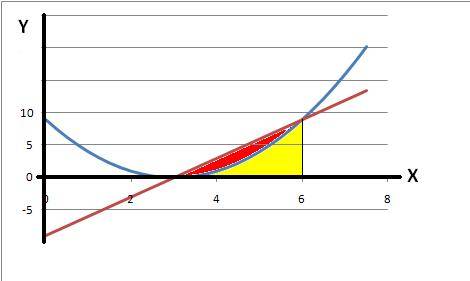
Линии, пересекаясь, образуют фигуру закрашенную на рисунке красным цветом. Чтоб найти ее площадь нужно из площади треугольника под прямой вычесть площадь под параболой, закрашенную желтым.
Эта площадь равна опр..интегралу в пределах (3,6) от
y=x^2-6x+9
интеграл будет 1/3x^3-3x^2+9x
в точке 6 он равен 72-108+54=18
в точке 3 он равен 9-27+27=9
Разность составляет 9
Значение функций в точке 6 равно 3*6-9=9
Площадь треугольника 9*3/2=13,5
Площадь искомой фигуры:
13,5-9=4,5
ответ 4,5
lim x->бесконечность (21x^3+x2+8)/x^3+x^2-8x= неопределенность типа (бесконечность/на
бесконечность), [чтобы избавиться от
неопределенности, нужно разделить на
наибольшую степень х, т.е. на х^3, получаем]
=lim x->бесконечность (21+1/x+8/х^3)/(1+1/x-8/x^2)= [подставляем вместо х бесконечность,
учитывая, что число, деленное на
бесконечность равно 0, получаем]
=21/1=21
скорость по течению реки=45.6+3.4=49км/ч
скорость против течения =45.6-3.4=42.2км/ч
2*49+3*42.2=98+126.6=224.6км