1. Метод исключения неизвестных.
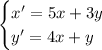
Продифференцируем первое уравнение:
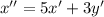
Подставим выражение для y':
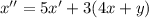
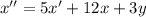
Из получившегося уравнения отнимем первое уравнение системы:
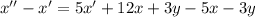
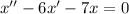
Составим характеристическое уравнение:
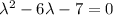
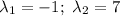
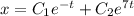
Найдем производную:
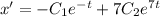
Выразим из первого уравнение системы у:
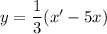
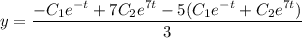
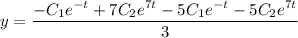
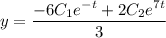
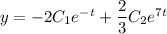
Общее решение:
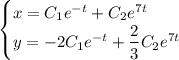
Находим решение задачи Коши:
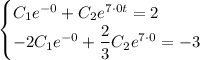
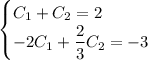
Первое уравнение домножим на 2:
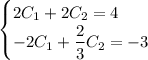
Сложим уравнения:
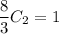
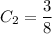
Выразим 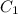 :
:

Частное решение:
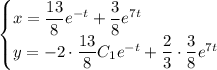
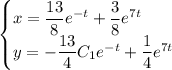
2. Метод характеристических уравнений (метод Эйлера).
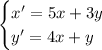
Матрица из коэффициентов при неизвестных:
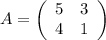
Характеристическая матрица:
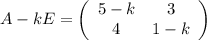
Характеристическое уравнение:
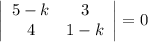
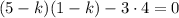
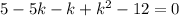
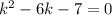
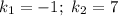
Общее решение:
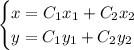
Ищем фундаментальную систему решений:
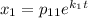
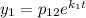
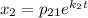
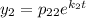
Для нахождения чисел 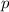 составим систему:
составим систему:
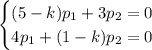
Для 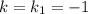 :
:
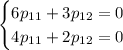
Оба уравнения дают:
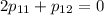
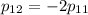
Найдем ненулевое решение. Пусть 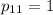 . Тогда
. Тогда 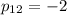 .
.
Для 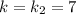 :
:
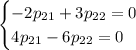
Оба уравнения дают:
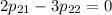
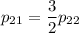
Найдем ненулевое решение. Пусть 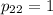 . Тогда
. Тогда 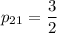 .
.
Фундаментальная система решений найдена:
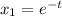
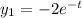
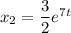
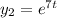
Общее решение:
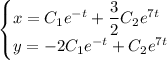
Находим частное решение:
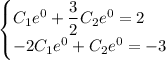
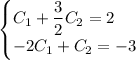
Первое уравнение домножим на 2:
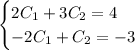
Сложим уравнения:
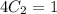
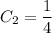
Выразим 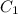 :
:
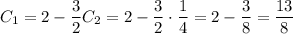
Частное решение:

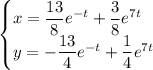
ответ:Пропорция — это равенство двух отношений.
Например, отношения \frac{6}{3} и \frac{8}{4} равны друг другу. Если соединить эти отношения равенством, то мы получим пропорцию:
\[\frac{3}{6} = \frac{8}{4}.\]
Эту пропорцию также можно записать так:
\[3 : 6 = 8 : 4.\]
В пропорции выделяют крайние и средние члены. Например, в пропорции 3 : 6 = 8 : 4 крайними членами являются числа 3 и 4, а средними членами — числа 6 и 8.
Основное свойство пропорции
Если пропорция составлена верно, то верно следующее утверждение:
Произведение крайних членов пропорции равно произведению средних.
То есть если пропорция
\[\frac{a}{b} = \frac{c}{d}\]
верна, то
Пошаговое объяснение: читай внимательно и поймеш как делать