После возведения в квадрат получим:
1) Sin² x = 2Cos x - 0,25
1 - Cos² x -2Cos x + 0,25 = 0
-Cos² x - 2Cos x +1,25 = 0
Решаем как квадратное по чётному коэффициенту:
Cos x = (1 +-√2,25)/-1 = (1 +-1,5) /-1
а)Cos x = -2,5 б) Cos x = -1/2
нет решений х = +- arcCos(-1/2) + 2πк, к∈Z
x = +- 2π/3 + 2πк, к ∈Z
2) Теперь проверяем промежуток
к = -1
х = 2π/3 - π (не входит в промежуток)
х = -2π/3 - π( не входит в промежуток)
к = -2
х = 2π/3 - 2π ( не входит в промежуток)
х = - 2π/3 - 2π = -8π/3 ( входит в промежуток)
к = -3
х = 2π/3 - 3π = -2 1π/3 (входит)
х =- 2π/3 - π - 1 2/3 π( входит)
к = -4
х = 2π/3 - 4π = - 3 1/3π (входит)
х =- 2π/3 - 4π (не входит)
к = -5
х = 2π/3 - 5π= - 4 1/3 π( входит)
х =- 2π/3 -5 π (не входит)
Пошаговое объяснение:
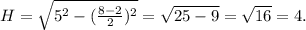
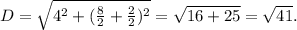
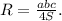
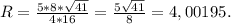
кут ВСК=куту СКД як внутрішні різносторонні також вони дорівнюють куту КСД тому що бісектриса поділила їх і т.д)
Тоді трикутник КСД-рівнобедренний оскільки кути при основі рівні.
Тоді СД=КД=5 см
Ну тоді периметр:
Р=10+22=32см)