Пошаговое объяснение:
В треугольнике АВС, В- является высотой. Если из вершины В провести биссектрису ВН, то угол АВН= углу СВН. Угол ВАН = углу ВСН (т.к. треугольник равнобедренный)
ВА=ВС (т.к. треугольник равнобедренный)
Треугольник ВАН = треугольнику ВСН по двум углам и стороне между ними
АН = НС (т.к. треугольник ВАН = треугольнику ВСН)
Т.к. медиана это отрезок делющий противолежащую сторону попалам, то ВН в равнобедренном треугольнике АВС является медианой
Угол АНВ =углу СНВ (т.к.треугольник ВАН = треугольнику ВСН)
АС- развернутый угол =180°
180°/2=90° = угол АНВ и углу СНВ (т.к.треугольник ВАН = треугольнику ВСН)
Т.к. высота-это отрезок опущенный перпендикулярно на противолежащую сторону, то он образует угол в 90° при соприкосновение с противолежащий стороной
1)две дроби называются равными если числители и знаменатели дробей равны: 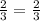 ;
;
2)из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше: 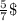 >
> ;
;
3)из двух дробей с одинаковыми знаменателями меньше та, у которой числитель меньше: 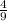 <
<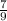 ;
;
4) из двух дробей с одинаковыми числителями больше та, знаменатель которой меньше:  >
>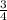 ;
;
5)любая правильная дробь меньше одной целой: 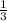 <1;
<1;
6)любая правильная дробь больше одной целой:  >1
>1
7)любая правильная дробь меньше любой неправильной дроби: 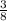 <
<
Пошаговое объяснение:
Воспользуемся диагоналями и высотой: d₁, d₂,Н.
d₁*H =3,
d₂*H =6,
d₁*d₂/2 = 1. Здесь пользуемся формулами площади прямоугольника( это диагональные сечения) и формулой площади ромба.
Решаем эту систему. d₁=3/H, d₂ = 6/H.
(3/H *6/H)/2 = 1
18/(2H²) =1, H² = 9, H=3. Можно найти объем V=S*H = 1*3 = 3 м³.
d₁=1, d₂ =2. Сторону ромба найдем из прямоугольного треугольника, образованного половинками диагоналей а =√(0,5² + 1²) = √(5/4) = 0,5√5.
Периметр ромба 0,5√5 *4 = 2√5.
Боковая поверхность Р*Н = 2√5*3 = 6√5. Добавляем площадь двух оснований. 6√5+2. Это полная поверхность.