у = 6 - x²; y = 0; x = 1; x = 3
6 - x² = 0 ⇒ x₁ = √6; x₂ = -√6
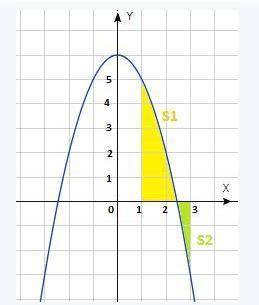
Ноль функции x₁ = √6 входит в интервал интегрирования
x₁ ∈ [1; 3] и разбивает криволинейную трапецию на 2 части : над осью Ох ( на графике залита жёлтым цветом ) и под осью Ох ( на графике залита зелёным цветом ). Общая площадь будет состоять из суммы двух площадей.
1) Площадь ограничена сверху параболой y = 6 - x², снизу осью абсцисс, слева прямой x = 1, справа нулём функции x₁ = √6.
2) Площадь ограничена снизу параболой y = 6 - x², сверху осью абсцисс, слева нулём функции x₁ = √6, справа прямой х = 3.
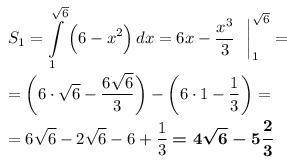
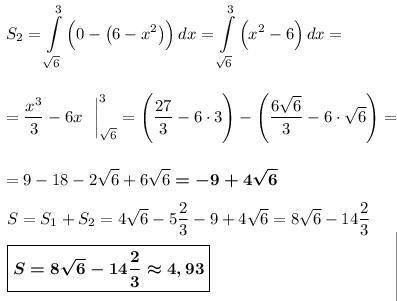
НОД (220; 280) = 20
НОК (220; 280) = 3080
Пошаговое объяснение:
Чтобы найти НОД чисел, нужно перемножить общие множители данных чисел.
разложим числа на простые множетели:
220 = 2 · 2 · 5 · 11
280 = 2 · 2 · 2 · 5 · 7
теперь перемножим их общие множители:
НОД (220; 280) = 2 * 2 * 5 = 20
Чтобы найти НОК чисел, надо к недостающим множителям меньшего числа добавить множители бОльшего числа и перемножить их.
разложим числа на простые множетели:
280 = 2 * 2 * 2* 5 * 7
220 = 2 * 2 * 5 * 11
теперь к недостающим множителям меньшего числа добавим множители бОльшего числа и перемножим их:
НОК (220; 280) = 2 * 2 * 2 * 5 * 7 * 11 = 3080
Решение:
Составим характеристическое уравнение
λ²-5λ+4=0,
D=5²-4·4=25-16=9,√√D=3, λ₁=(5+3)/2=4,λ₂=(5-3)/2=1
Тогда общее решение уравнения имеет вид:
у(х)=C₁eˣ+C₂e⁴ˣ
2.yy'+x=0
Разделим каждое слагаемое на у·у'=-x, y'=dy/dx,тогда имеем
у·dy/dx=-х или у·dy=-х·dx .Интегрируем обе части последнего уравнения:
∫уdy=-∫хdx или у²/2=-х²/2+С=С-х²/2
у₁=-√ С₁-х² и у₂=√С₁-х²
Решением будет:у(х)=-√( С₁-х²) у(х)= √( С₁-х²)
3.M(x)=8
D(x)=4
2 < x<14
p(2<x<14)-?
Решение:
Имеем q=√D=√4=2.
p(α<x<β)=Ф((β-а))/Q-Ф((q-a)/Q)
p(2<x<14)=
Ф((14-8))/2-Ф((2-8)/2)=Ф(3)+Ф(3)=
=2Ф(3)=2·0.0044=0.0088
ответ:0.0088