5; 8
Пошаговое объяснение:
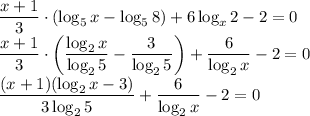
ОДЗ: x > 0, x ≠ 1
Учитывая ОДЗ, домножим уравнение на 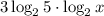 , а также обозначим
, а также обозначим 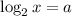 для удобства:
для удобства:
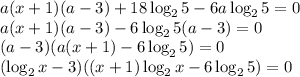
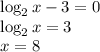
ИЛИ
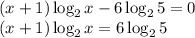
На промежутке x > 1 слева представлено произведение двух положительных монотонно возрастающих функций. Значит, на данном промежутке левая часть — монотонно возрастающая функция, принимающая каждое значение ровно один раз. Значит, при x > 1 уравнение имеет не более одного корня. Действительно, при x = 5 равенство выполняется.
На промежутке 0 < x < 1  . На данном промежутке решений быть не может. Остальные промежутки числовой оси не удовлетворяют ОДЗ.
. На данном промежутке решений быть не может. Остальные промежутки числовой оси не удовлетворяют ОДЗ.
Таким образом, уравнение имеет два решения: 5 и 8.
(см. объяснение)
Пошаговое объяснение:
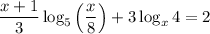 , ОДЗ:
, ОДЗ: 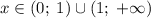 .
.
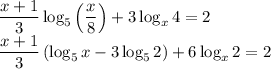
Выполним замену 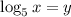 . Тогда
. Тогда 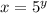 .
.
Заметим сразу, что 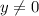 , так как
, так как 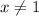 .
.
Тогда уравнение примет вид:
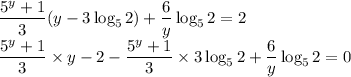
Так как 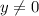 , то верно, что
, то верно, что 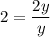 .
.
С учетом этого перепишем уравнение:
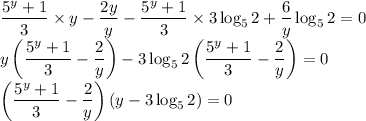
Тогда перейдем к совокупности:
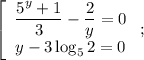
Рассмотрим первую строку совокупности:
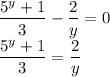
Слева показательная функция. Она монотонно возрастает.
Справа гипербола. Она убывает на всей области определения.
Тогда рассматриваемое уравнение может иметь не более одного корня.
Несложно увидеть, что это 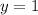 , так как при нем равенство верно.
, так как при нем равенство верно.
Рассмотрим вторую строку совокупности:

Выполним теперь обратную замену:
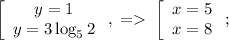
Так, учитывая ОДЗ, мы получили, что 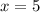 и
и 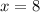 - это корни исходного уравнения.
- это корни исходного уравнения.
Задание выполнено!
⇒ 8,9+а=9,5·2 ⇒ а=(9,5·2)-8,9
а=19-8,9=10,1
а=10,1
Проверка:
(8,9+10,1):2=9,5