Красный
Пошаговое объяснение:
Если вытащили 2 белых шара, то кладут 1 белый.
Количество белых уменьшается на 1, красных не меняется.
Если вытащили 2 красных шара, тоже кладут 1 белый.
Количество белых увеличилось на 1, красных уменьшилось на 2.
Если вытащили белый и красный шары, то кладут красный.
Количество белых уменьшается на 1, красных не меняется.
Таким образом, четность красных шаров не меняется, а четность белых меняется на каждом шагу.
Так как в начале красных шаров 2017, то есть нечетное количество, то оно и останется нечетным, то есть упадет до 1.
Красный шар и будет последним.
Пошаговое объяснение:
1) Сначала определим количество выборов стульев для гостей.
Пусть из множество A берется сразу несколько элементов. В результате такого одновременного неупорядоченного выбора k элементов из множества A, состоящего из n элементов, получаются комбинации выбора), которые называются сочетаниями без повторений из n элементов по k (количество выбора).
Число сочетаний из n элементов по k обозначается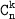 
и равно:
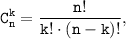
где m!=1·2·3·...·(m-1)·m.
Тогда, по условию задачи общее количество стульев n=8 и нужно выбрать стульев k=4:
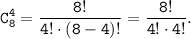
2) Теперь определим количество рассадки 4-х гостей на 4-х стульях. Так как каждый вариант рассадки отличается только порядком участников, то есть является перестановкой из 4 элементов:
P₄=4!.
3) Количество необходимых для рассадки 4-х гостей на 8-ми стульях определим как произведения число сочетаний на перестановку:
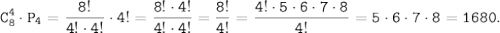
2x+3,6=12,8
2x=12,8-3,6
2x=9,2
x=9,2:2
x=4,6