АЕ = 11 ед.
Пошаговое объяснение:
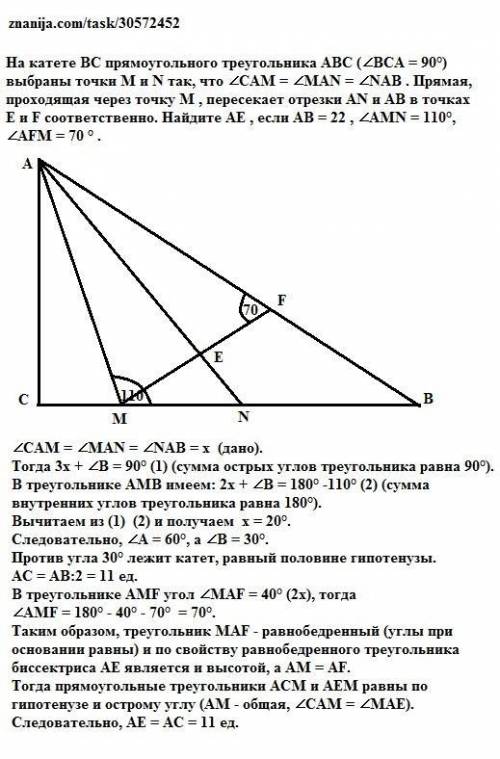
∠CAM = ∠MAN = ∠NAB = х (дано).
Тогда 3х + ∠В = 90° (1) (сумма острых углов треугольника равна 90°).
В треугольнике АМВ имеем: 2х + ∠В = 180° -110° (2) (сумма внутренних углов треугольника равна 180°).
Вычитаем из (1) (2) и получаем х = 20°.
Следовательно, ∠A = 60°, а ∠В = 30°.
Против угла 30° лежит катет, равный половине гипотенузы.
АС = АВ:2 = 11 ед.
В треугольнике АМF угол ∠MAF = 40° (2х), тогда
∠AMF = 180° - 40° - 70° = 70°.
Таким образом, треугольник MAF - равнобедренный (углы при основании равны) и по свойству равнобедренного треугольника биссектриса АЕ является и высотой, а АМ = AF.
Тогда прямоугольные треугольники АСМ и АЕM равны по гипотенузе и острому углу (АМ - общая, ∠CAM = ∠MAЕ).
Следовательно, АЕ = АС = 11 ед.
Площадь каждого прямоугольника равна 32 дм2
1. 32:4=8 дм
2. 8:2=4 дм
3. 8х4=32 дм2
Пошаговое объяснение:
Из условия следует, что периметр квадрата равен 32 дм. Периметр - это сумма всех сторон фигуры. У квадрата их 4 и они равны между собой. Вычисляем длину каждой стороны квадрата путем деления периметра на кол-во его сторон: 32:4=8 дм.
Далее из условия следует, что прямоугольники одинаковые, их два и они составляют квадрат (вписаны в него). Значит одна из их сторон равна 8 дм, как и найденная длина стороны квадрата, а другие стороны прямоугольника составляют половину стороны квадрата, т.е.
8:2=4 дм
Стороны прямоугольника составляют два коротких ребра = 4дм, и два длинных ребра = 8 дм. Площадь такой фигуры будет равна произведению двух его сторон:
8х4=32 дм2
Для нахождения длин сторон используем теорему синусов.
Аналогично находим АС = 27.11503.