ответ во вложении.........
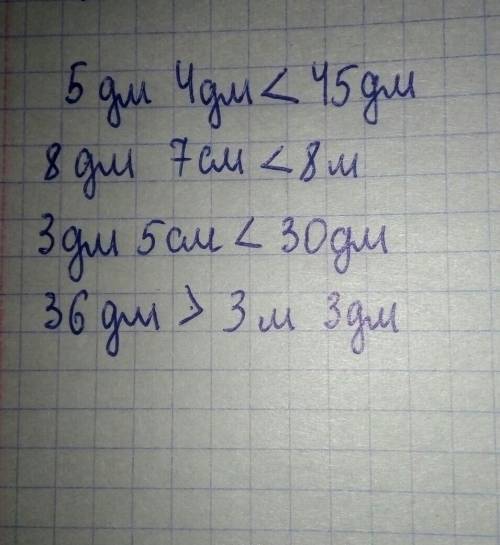
3. А) Расходится
lim (n/6n+4)
n→+∞
lim (n/n×(6+4/n))
n→+∞
lim(1/6+4/n)
n→+∞
1/6+4×0 = 1/6
Б) Расходится
lim ( | (n+1+1)! / 9^n+1 / (n+1)! / 9^n | )
n→+∞
lim ((n+2)! / 9^n+1 / (n+1)! / 9^n)
n→+∞
lim( (n+2)! / 9×(n+1)! )
n→+∞
lim ( (n+2)×(n+1)! / 9×(n+1)! )
n→+∞
lim (n+2/9)
n→+∞
lim (1/9 × (n+2) )
n→+∞
1/9 × lim (n+2)
n→+∞
+∞
4. f 1/2×(cos(-6x)+cos(10x))dx
f 1/2×(cos6x+cos10x)dx
½ × f cos6x+cos10x dx
½ ( f cos6xdx + f cos10xdx)
½ (sin6x/6 + sin10x/10)
sin6x/12+sin10x/20 + C, C€R
5. A) Сходится
lim (1/3n+1)
n→+∞
lim (1) lim(3n+1)
n→+∞ n→+∞
1 +∞
Выражение а/±∞ определено как 0
1/3n+1 ≥ 1/3(n+1)+1
Истина
Б) Сходится
lim ( 1/(n+17)!)
n→+∞
lim (1) lim((n+17)!)
n→+∞ n→+∞
1 +∞
a/±∞ определено как 0, поэтому 0
1/(n+17)! ≥ 1/(n+1+17)!
Истина
Предположим обратное, то есть то, что невозможно окружности совместить так, чтобы ни одна отмеченная точка не попала на отмеченную дугу.
Совместим окружности. Назовем 
-тую точку 
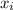. Будем действовать следующим образом: в начальный момент хотя бы одна точка находится на дуге (пусть это точка 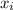). Начнем движение одной окружности относительно другой. Как только точка 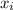сойдет с дуги, переключим внимание на другую точку 
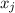, которая в этот момент находится на дуге. В каждый момент считаем прибором расстояние, которое проходит точка, за которой мы наблюдаем. Поэтому мы посчитаем расстояние 
, не превосходящее 
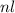, где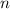 
— количество точек, 
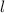— суммарная длина дуг. С другой стороны, в любой момент прибор включен и считает расстояние. Поэтому не меньше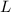 
— длины окружности. Имеем: 
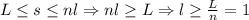, однако 
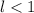. Противоречие.
5 дм 4 дм < 45 дм
8 дм 7 см > 8 м
3 дм 5 см < 30 дм
36 дм > 3 м 3 дм